- 1,753
- 143
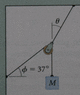
A box of mass M = 5.7 kg is suspended by a rope over a pulley (Figure 5.64). Find the tension in the rope supporting the box and in the rope supporting the pulley.
The tension in the rope supporting the box should just be mg? right?
But the two labeled angles are not the same. Combined, they must be equal to -mg or the pulley would accelerate. But without knowing theta angle, I'm not sure how to do this? Do they want the tension of the rope supporting the pulley to be expressed in terms of something else, or is it possible to come up with a precise number in Newtons?
The tension in the rope supporting the box should just be mg? right?
But the two labeled angles are not the same. Combined, they must be equal to -mg or the pulley would accelerate. But without knowing theta angle, I'm not sure how to do this? Do they want the tension of the rope supporting the pulley to be expressed in terms of something else, or is it possible to come up with a precise number in Newtons?