You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
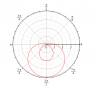
Finding the Area Enclosed by a Polar Curve
Physics news on Phys.org
LCKurtz
Science Advisor
Homework Helper
- 9,567
- 775
amninder15 said:Can someone please help me on this question. I tried to solve it by integrating 0.5*(1-3sin(θ)^2 from -Pi/2 to 0 but I didnt get the answer.
Why did you choose ##-\frac \pi 2## to ##0##? Just guessing? Have you drawn a sketch? Do you know what ##\theta## give negative ##r## values for the inner loop?
DryRun
Gold Member
- 837
- 4
Your graph is correct for ##\theta## varies between 0 and 2pi. Now, generally how do you find the area of a polar region?
LCKurtz
Science Advisor
Homework Helper
- 9,567
- 775
amninder15 said:Yea I made some silly mistake I think It goes from sin^-1(1/3) to Pi-sin^-1(1/3). But that looks ugly. Am I on right path.
Yes. Those are the correct limits. Ugly or not, just plow ahead and you will get one of the answers listed.
Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$
Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$
The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$
Plugging identity above into ##(1)## with ##u...
Similar threads
- Replies
- 3
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 19
- Views
- 2K
- Replies
- 13
- Views
- 5K
- Replies
- 8
- Views
- 2K
- Replies
- 10
- Views
- 3K
- Replies
- 2
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 1K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 105
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
-
Finding the modulus and argument of ##\dfrac{a}{(b±ci)^n}##
- Started by chwala
- Replies: 17
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math