Finding the area of a double integral using dxdy instead of dydx

[ago01]

Homework Statement

Given The curve $$y = e^x$$ and the lines $$y = 0$$, $$x = 0$$, and $$x = ln 2$$ express the area as an iterated integral and solve.

Relevant Equations

N/A

I have the solution for this problem using dydx as the area. Worse yet, I cannot find another solution for it. Everyone seems to just magically pick dydx without thinking and naturally this is frustrating as learning the correct choice is 99.9% of the battle...

So, I was curious how one might go about solving it the other way. Here's a representation of the area:

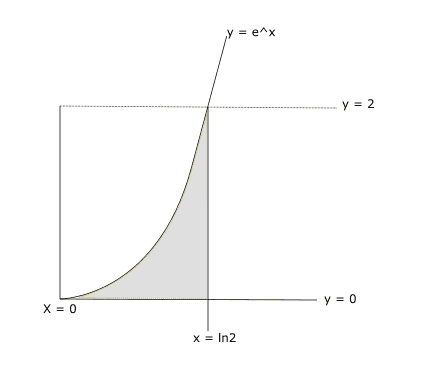
So if we imagine going from left to right (for dx) then our x limits seem to go from $$y=e^x$$ to $$ln2$$ which implies $$x = lny$$ and $$x = ln2$$ for our lower and upper limits. Then it follows that y goes from $$0$$ to $$2$$. So:

$$\int^{2}_{0}\int^{ln2}_{lny}dxdy$$

But after solving this integral I get an area of 2, rather than the desired area of 1. I cannot figure out how my setup is wrong here. What am I missing?

 

[Orodruin]

The graph of $y = e^x$ does not look like your drawing of it.

 

[ago01]

I see. Yeah that would do it. e^x has y = 1 at x = 0. My graph is shoddy.

It's obvious now that if you go the x-direction you have two different functions. One being x= 0, and then it switches to y = e^x. In this case, you would need extra integration to cover that function switch, so dydx is really the only way to do it.

 

[vela]

You, of course, should know how to do it either way. So I wouldn't say using $dy\,dx$ is the only way to do it, but perhaps the preferable way to do it.

If you integrate with respect to $x$ first, you still really only need one integral since the other chunk of the area is a rectangle. You don't need to integrate to find its area.

 

[nuuskur]

The desired area is
$$\int _0^{\ln 2} e^x \mathrm{d}x = e^{\ln 2} - e^0 = 1.$$
You can regard this area as a double integral as follows.
$$\int\int _A \mathrm{d}y\mathrm{d}x = \int _0 ^{\ln 2} \int _0^1 \mathrm{d}y\mathrm{d}x + \int _0^{\ln 2} \int _1^{e^x}\mathrm{d}y\mathrm{d}x = \ln 2 + \int _{0}^{\ln 2}(e^x-1)\mathrm{d}x = 1.$$
Equivalently,
$$\int\int _A \mathrm{d}x\mathrm{d}y = \int _0^1 \int_0^{\ln 2} \mathrm{d}x\mathrm{d}y + \int _1^2 \int _{\ln y}^{\ln 2} \mathrm{d}x\mathrm{d}y = \ln 2 + \int _1^2 (\ln 2 - \ln y)\mathrm{d}y = 1.$$
You need more effort to use quantities like $\int _a^b \ln x\mathrm{d}x$.

Spoiler

That's why the invariance is often extremely useful, because in a certain order, computation could be significantly easier. Due to said invariance, one may conclude that
$$\int _1^2 \ln y\mathrm{d}y = \ln 4 -1$$
without explicit computation. Sometimes one order might include an integral for which an antiderivative in terms of elementary functions is not known, but another order is trivial.

You might have thought that
$$\int _0^2 \int _{\ln y} ^{\ln 2} \mathrm{d}x\mathrm{d}y = \int _0^1 \int _0^{\ln 2}\mathrm{d}x\mathrm{d}y + \int _1^2 \int _{\ln y}^{\ln 2} \mathrm{d}x\mathrm{d}y$$
but as we saw, this is not true. Why? Because on the left hand side, $y$ is allowed to range from $0$ and $\ln y$ is unbounded as $y\to 0+$ so the left hand side does not correspond to the area of interest.

The LHS allows you to compute the area under $e^x$ where $-\infty < x < \ln 2$, which explains your result of $2$.