Finding the current and the voltage across each resistor

AI Thread Summary
The discussion focuses on calculating the current and voltage across each resistor in a circuit with a total voltage of 24V and four resistors: R1 (270 ohms), R2 (330 ohms), and two R4 (1.2k ohms). Participants clarify that R1 and R2 are in series with the combined resistance of the two 1.2k ohm resistors, which are in parallel. The effective resistance of the parallel resistors is calculated to be 600 ohms, leading to a total resistance of 300 ohms when combined with R1 and R2. The provided current values for each resistor are confirmed, but the method to derive these values is discussed and clarified. Understanding the series and parallel relationships is crucial for solving the circuit correctly.
Lopez
Messages
8
Reaction score
0

Homework Statement


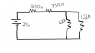
Find the current and the voltage across each resistor.

volts is 24v
R1=270 ohms
R2=330 ohms
R2=1.2k ohms
R4=1.2k ohms


Homework Equations





The Attempt at a Solution


This is not a homework its more like a study guide.
He gave us the answer for just the currents which are
IR1=20
IR2=20
IR3=10
IR4=10
But not sure how he got that.
this is what i did but don't know how to go from there:
(270+330)|| (1.2k||1.2k)
600||600
R=300
 

Attachments

  • practice.png
    practice.png
    8.2 KB · Views: 526
Physics news on Phys.org
Hi Lopez. Welcome to physics forums!

The 270 and 330 are in series with the 600, not parallel.

Chet
 
Lopez said:
(270+330)|| (1.2k||1.2k)
Having reduced the (1.2k||1.2k) to an effective 0.6k, what is the relationship of that in the circuit to R1 and R2?
 
ahh yes there was the problem,after 1.2 k and the other 1.2k were combined it becomes one resistor in series with the (r1 and R2). Thanks!
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Calculating the voltage across capacitors and resistors with switches
Replies
2
Views
735
Ohm's Law - Finding Source Voltage
Replies
3
Views
1K
Reducing voltage with two resistors
Replies
4
Views
2K
Using Current and Voltage Dividers
Replies
3
Views
1K
Voltage drop and current through each resistor
Replies
3
Views
2K
Voltage, Current, and Resistance Calculations
Replies
13
Views
2K
Finding the Current in a Resistor in a Closed Circuit
Replies
4
Views
2K
How do I calculate voltage drops and currents in a resistor circuit problem?
Replies
4
Views
2K
Parallel circuit with internal resistance
Replies
6
Views
2K
Find currents and voltages - 2 batteries & 3 resistors
Replies
3
Views
4K

Hot Threads

Recent Insights

Back
Top