Finding the decrease in potential energy of atwood machine

In summary, when an object of mass m2 has descended a distance h in a system where m1<m2, the potential energy of the system decreases by (m2-m1)gh. This can be calculated using the equation ΔU = Uf - Ui, where Uf is the final potential energy and Ui is the initial potential energy. The answer may seem to have the two masses in reversed order, but this is because you have found the increase in GPE, whereas the question specifically asks for the decrease.
  • #1
Davyd Sadovskyy
3
0

Homework Statement


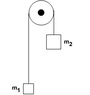
In the system below, m1<m2. When the object of mass m2 has descended a distance h, the potential energy of the system has decreased by:
upload_2017-11-3_21-10-29.png


Homework Equations


the answer is (m2-m1)gh

The Attempt at a Solution


I used ΔU= Uf-Ui

m1gh-m2gh=ΔU (I think that the decrease in potential energy is equal to the change in Ug because at the final configuration, m1 is at the same height that m2 is at initially, but has less weight, so the potential energy must decrease from start to finish)

gh(m1-m2)

why does the answer have the two masses in reversed order. pls help
 

Attachments

  • upload_2017-11-3_21-10-29.png
    upload_2017-11-3_21-10-29.png
    921 bytes · Views: 852
Physics news on Phys.org
  • #2
Davyd Sadovskyy said:
why does the answer have the two masses in reversed order.
because you found ΔU, the increase in GPE, whereas the question asks for the decrease.
 

1. How does an Atwood machine work?

The Atwood machine is a simple mechanical device consisting of a pulley, two masses, and a string. The two masses are connected by the string which passes over the pulley. When one mass is released, its weight causes it to accelerate towards the ground while the other mass moves upward. This creates a difference in potential energy between the two masses, causing them to move towards each other.

2. What is the formula for calculating the decrease in potential energy of an Atwood machine?

The formula for calculating the decrease in potential energy of an Atwood machine is: ΔPE = mgh, where m is the difference in mass between the two masses, g is the acceleration due to gravity, and h is the height difference between the two masses.

3. How can the decrease in potential energy of an Atwood machine be used in scientific experiments?

The decrease in potential energy of an Atwood machine can be used in experiments to study the relationship between mass, acceleration, and gravity. It can also be used to demonstrate the principle of conservation of energy.

4. What factors affect the decrease in potential energy of an Atwood machine?

The decrease in potential energy of an Atwood machine is affected by the difference in mass between the two masses, the acceleration due to gravity, and the height difference between the two masses. Friction and air resistance can also affect the decrease in potential energy.

5. How is the decrease in potential energy of an Atwood machine related to the work done by the system?

The decrease in potential energy of an Atwood machine is equal to the work done by the system. This means that the decrease in potential energy can be calculated by multiplying the applied force by the distance the mass has moved. In other words, the decrease in potential energy represents the amount of work done by the system in moving the masses.

Similar threads

Double Atwood Machine Problem
    • Introductory Physics Homework Help
Replies
1
Views
3K
Atwood Machine: Find M in Terms of m1 & m2
    • Introductory Physics Homework Help
Replies
3
Views
1K
Negative Moment of Inertia from Atwood Machine Experiment?
    • Introductory Physics Homework Help
Replies
13
Views
3K
Potential Acceleration of an Atwood Machine
    • Introductory Physics Homework Help
Replies
7
Views
2K
Kinetic energy of a compound system (atwood machine)
    • Introductory Physics Homework Help
Replies
1
Views
1K
An Atwoods Machine hanging from the ceiling
    • Introductory Physics Homework Help
Replies
29
Views
4K
Atwood machine with variable mass
    • Introductory Physics Homework Help
Replies
7
Views
3K
Energy conservation for objects hanging from a pulley
    • Introductory Physics Homework Help
Replies
6
Views
2K
Need Help finding theoretical and actual acceleration (Atwood)
    • Introductory Physics Homework Help
Replies
9
Views
5K
Atwood with Sliding mass and real pulley
    • Introductory Physics Homework Help
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top