Finding the density of a block in two layers of liquids

[Akash47]

Homework Statement

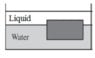
A layer of liquid with density $800~kg/m^3$ floats on top of a volume of water. A block floats at the oil-water interface with $3/4$ of it in water and the rest of it in the liquid. What is the density of the block?

Homework Equations

Buoyancy =$vρg$ where $v$= volume of the block, $ρ$=density of liquid, $g$=gravitational acceleration.

The Attempt at a Solution

(maybe the solution)The block has displaced water of volume of $3/4$ times the block's volume, so buoyancy on it by water is $3/4~vρ_wg$ ($ρ_w$=density of water) which is acting upward.The block has displaced liquid of volume of $1/4$ times the block's volume,so buoyancy acting on it by the liquid is $1/4~vρ_lg$ ($ρ_l$=density of the upper liquid) which is acting upward.We assume downward as negative and upward as positive.The weight of the block is $vρ_bg$ where $ρ_b$=density of the block.The block is in stating equilibrium,so
$3/4~vρ_wg+1/4~vρ_lg=vρ_bg$ implies, $3/4~v*1000*9.8~+1/4v*800*9.8= vρ_b*9.8$
So, $ρ_b=950$.

 

[stockzahn]

So, $ρ_b=550$.

If the density of the block would be smaller than the density of the oil, wouldn't the block float on the oil?

Different question: Where does a balance show a larger value measuring your weight: In your bathroom filled with air or if it is evacuated?

 

[Akash47]

Oh,I got my fault.As I have got the density of the block less than the liquid,so the block should float on the surface but that's against the condition.Then the buoyancy force on the block by the upper liquid may be acting upward.Thus I get the density of the block is $950~kg/m^3$(see the edited thread) and that may satisfy the condition mentioned in question.But if the liquid forces the block upward,then the bottom of the block should be in the liquid but it's bottom surface is in the water.Then how it's possible?

 

[Chestermiller]

Let h represent the depth of the liquid and H be the thickness of the block. What is the liquid pressure at the top of the block? What is the water pressure at the bottom of the block? If A is the cross sectional area of the block, what is the liquid downward force on the top of the block? What is the water upward force on the bottom of the block?

 

[stockzahn]

Thus I get the density of the block is $950~kg/m^3$

That looks good

But if the liquid forces the block upward,then the bottom of the block should be in the liquid but it's bottom surface is in the water.Then how it's possible.

Image you are swimming in the ocean. You are floating, since the density of the salt water is higher than yours. But if you are at the beach you can stand in the water just with its level reaching e.g your knees. Although the density of the water is higher, you don't float, because the buoyancy force only is as high as the weight force of the displaced water. But you will weigh less by the volume of your legs below your knees multiplied by the density of the water (and the gravitational acceleration).

 

[haruspex]

But if the liquid forces the block upward,then the bottom of the block should be in the liquid but it's bottom surface is in the water

How is the oil pushing the block up when it only contacts the top and sides? (There is an answer.)
One needs to be a bit careful applying Archimedes' principle. It is only valid when the fluid can exert pressure on the entire surface of the body. E.g. consider a rubber suction cup stuck to the bottom of a tank.
It can be applied in this case since the oil exerts pressure on the water, and that pressure is transferred to the underside of the body by the water.

 

[Akash47]

Thanks to all of you for helping me specially Chestermiller and haruspex.