Joa Boaz
- 14
- 1
Homework Statement
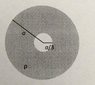
A charged insulating spherical shell has winner radius of a/3 an an outer radius of a. The cross section is as shown on the picture. The outer shell has a non-constant volume charge density of ρ = 6*α*r^3. Find the electric field magnitude in each region (outside the object, in the shell itself, and in the cavity contained in the shell). Find the electric potential in each region, and sketch a graph of the electric potential as a function of radius for r = 0 to r = 2a and label the potential at r = a/3, a, and 2a. The reference point for the potential is that V = 0 to r = ∞
Homework Equations
Not sure but,
E = (1/4∏*ε) * Q/r^2
E = (1/4∏*ε) * (Q/r^3) * r
The Attempt at a Solution
q(inside) = -Q(sphere) = - 4/3 * ∏ * (a^3) ρ = (-4/3)*∏*((a^6)/729)*6α = (-8/729)*(a^6)*∏*α
q(outise) = - q(inside) = (8/729)*∏*α
σ(outer) = q(outside)/4∏*a^2 = (2/729)*(a^4)*∏*α
Not sure if the above is correct, but I am not sure what I have to do after this. Please can anyone help, thank you.