Scholar1
- 39
- 0
Member warned about posting without the template
I have posted my attempt and the problem above. Please help!
Thanks in advance!
It's hard to mark up an image.Scholar1 said: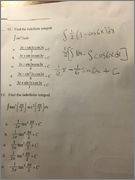
I have posted my attempt and the problem above. Please help!
Thanks in advance!
Yesss...multiplication distributes over addition and subtraction.Scholar1 said:So if I put - (1/12) in front of the sin6x it would be correct?