- #1
bieon
- 32
- 3
- Homework Statement
- Jane thinks that Tarzan has been gaining too much mass. However, he doesn’t want to tell her what he weighs. One day Tarzan is swinging in the forest. He starts from rest from one side at an angle of 53° from the vertical. He swings down and grabs Jane at the bottom of the swing. They swing together on the other side up to a maximum angle of 37 °. Jane knows that her mass is 50 kg. Calculate Tarzan’s mass. (Ans.120.8kg)
- Relevant Equations
- Refer Below.
My Attempt So Far:
1) Drawing a diagram based on the question.
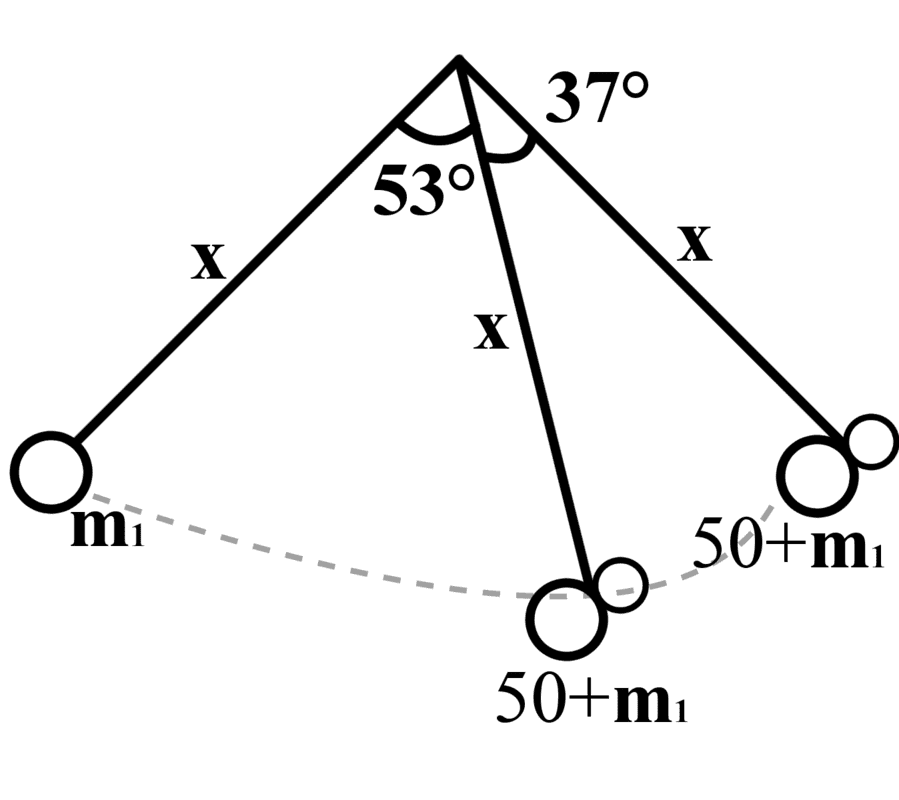
Diagram 1: Pendulum Diagram Based On Question
2) List down pieces of information found in the question.
θ1=53°
θ2=37°
m1=m1
m2=m1+50kg
vi=0
3) Since 53°+37°=90°, I redraw another diagram making it into a right angle triangle in order to find the length of the vine.
Since the length of the vine is the same in the initial location and final location, I assumed that the adjacent and opposite sides are equal.
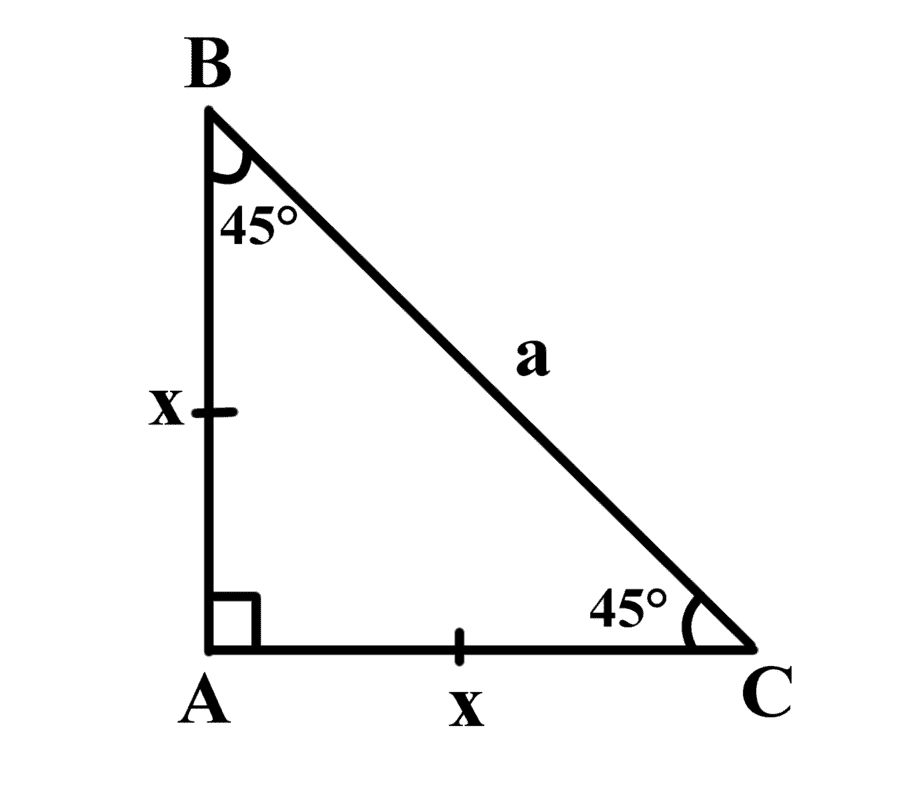
Diagram 2: Right-Angled Triangle Derived From Question4) I then tried to find the length of x by applying the Cosine Rule.
I was stuck from this point on... Any help is appreciated...
1) Drawing a diagram based on the question.
Diagram 1: Pendulum Diagram Based On Question
2) List down pieces of information found in the question.
θ1=53°
θ2=37°
m1=m1
m2=m1+50kg
vi=0
3) Since 53°+37°=90°, I redraw another diagram making it into a right angle triangle in order to find the length of the vine.
Since the length of the vine is the same in the initial location and final location, I assumed that the adjacent and opposite sides are equal.
Diagram 2: Right-Angled Triangle Derived From Question
c2=a2+b2-2ab(cos C)
Equation 1: Cosine Rule
x2=a2+x2-2ax(cos 45)
Substitute the unknowns with the numbers or unknowns that are shown in the diagram drawn.
-a2=-2ax(cos 45)
Cancel like terms and try to put everything in term of a
a=√2 x
Let this equation be the first equation.
5) After getting the first equation, I tried finding the length of the vine by using sin θ = Opposite/HypotenuseEquation 1: Cosine Rule
Substitute the unknowns with the numbers or unknowns that are shown in the diagram drawn.
-a
Cancel like terms and try to put everything in term of a
a=√2 x
Let this equation be the first equation.
sin 45 = x/a
sin 45 = x/√2 x
sin 45 = √2/2
√2=x
2=a
sin 45 = x/√2 x
sin 45 = √2/2
√2=x
2=a
I was stuck from this point on... Any help is appreciated...