Finding the moment(s) of inertia

[dinospamoni]

Homework Statement

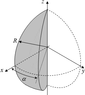
A wedge of a sphere of radius 14 cm (similar to one
segment of an orange) is oriented so that the axis is aligned
with the z-axis, one face is in the xz plane, and the other
is inclined at an angle of α = 29o
, as shown. The wedge is
made of metal having a density of 4500 kg/m3
. In the coordinate system shown, compute a) Ixx, b) Iyy, and c) Izz.

The picture is attached

Homework Equations

I know that

I_xx= ∫(y^2+z^2)ρ dV
I_yy= ∫(x^2+z^2)ρ dV
I_zz= ∫(y^2+y^2)ρ dV

The Attempt at a Solution

I'm having trouble thinking of how to replace the dV with something in terms of x y and z

The first thing I did was find the mass, but I'm not sure if it would help at all

I did V=4/3 π r^3

and then multiplied by 29/360 to find the volume of the wedge and the multiplied by the density.


Also, just thought of this now:

r = (x^2 + y^2 + z^2)^1/2

could I differentiate the volume equation to find dV in terms of r and dr (4 pi r^2 dr)
and substitute in the above expression for r and just tack on dx dy and dz? SOrry if that breaks all rules of physics

 

[mfb]

The first thing I did was find the mass, but I'm not sure if it would help at all

I did V=4/3 π r^3

and then multiplied by 29/360 to find the volume of the wedge and the multiplied by the density.

That does not help.
You can write dV = dx dy dz in cartesian coordinates. There are similar formulas for spherical coordinates and other coordinate systems.

could I differentiate the volume equation to find dV in terms of r and dr (4 pi r^2 dr)

y^2 + z^2 and similar expressions are not constant for constant r, this does not work. You will need more than 1 integral.

For I_zz, you can use the symmetry of the problem, if you know the moment of inertia of a ball.

 

[dinospamoni]

After posting this I converted it to spherical coordinates and used triple integration and found the correct answers. Thanks though!