Finding the period of a pendulum witha string that has mass

[Physics Man]

1. The problem statement, all variables and gihttps://www.physicsforums.com/attachments/218400 ven/known data
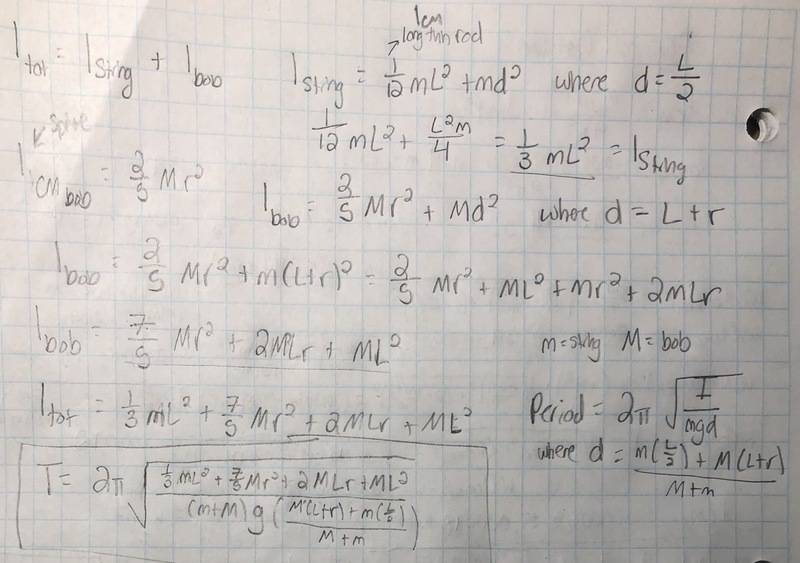
Assuming the string from a simple pendulum did not have negligible mass and the pendulum bob was not a point mass, then determine an expression for the period of a single small-amplitude oscillation, treating the string as a rigid rod.

Homework Equations

Theoretical moment of inertia of center of mass for long thin rod = 1/12 mL^2

The Attempt at a Solution

https://prnt.sc/i02al1 This is what I did but I don't think that it is right

 

[kuruman]

This is what I did but I don't think that it is right

Why not? Check if your equation reduces to the limiting case for which you know the answer, namely massless string and point-mass bob.

 

[haruspex]

solved

Please do not delete the post that initiated the thread.