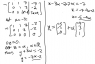gracelette
- 2
- 0
Homework Statement
given the planes with equations:
x + y + 7z = -7
2x + 3y + 17z = -16
x + 2y + (a^2 + 1) z = 3a
find values for the constant a for which:
-there are no solutions
-the planes meet in a line. in this case find the parametric equation of the line
-meet at a point. then find the parametric equation of the point.
Homework Equations
gaussian elimination? I don't think there are any. =S
The Attempt at a Solution
I put the planes into an augmented matrix, and then into echelon form, and got (I think its correct) the general solution, which is attached. From the I can read off the equation of the line, right? The parts I'm really stuck on are parts one and three. I realize that for the planes to meet in a point, there has to be 3 pivots but beyond that I'm a bit stumped.
Well actually, I have a bit of a clue for part one, that a =/= 3 because then 0z = 18 which is inconsistent. is that right? But for part 3, I'm not sure how to do it, really.
Attachments
Last edited: