Finding the Transfer Function of an RC Circuit in the Laplace domain

[zaka]

Hi,

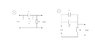
Basically I have circuit with an input Vi (s) across a capacitor C which is in parallel with a resistor R1. And these 2 components are in series with another resistor R2 (please see attached drawing).

The question states:

Show that the transfer function of the circuit is:

Vo/Vi = (s + (1/(R1.C))) / (s + (R1+R2)/(R1.R2.C)) (Hope that's clear)

Where the laplace voltage (drop) across each individual component is as follows:

V(s) = I(s) / sC [laplace of capacitor]

V(s) = I(s) . R [laplace of a resistor]



In a previous worked example, the Transfer function was found by using mesh analysis and Kirchhoff's second law to find an equivalent equation for Vi and Vo. Therefore I thought I could use that here.

In the attachment I've redrawn the circuit given in the question (which is on the left labeled (1)), so that there are 2 clear loops to use mesh analysis on (the right labeled (2)). Is this correct?

(1) is the diagram given in the question
and (2) is what I've redrawn (1) as.
(This is the first time I've come across a resistor in parallel with a capacitor and I'm guessing they both have the same voltage drop across them).



Anyway so what I did was as follows (using my attached equivalent drawing (2):

loop 1) Vi (s) = [I1(s) . R1] + [I1(s) . R2] - [I2(s) . R1]

loop 2) 0 = [I2(s) . R1] + [I2(s) / sC] - [I1(s) . R1]

I rearranged loop 2 equation to get I2(s) in terms of I1(s) and substituted that into loop 1 equation. I think this would be Vi. As for Vo I assumed that would just be the voltage drop across R2 which is I1(s) . R2.

However, I could not simplify my answer (whatsoever) to what the question gave, making me think that I've done something wrong.

Any help would be much appriciated. I hope everything above makes sense.

 

[rude man]

Why write these loop equations?

If you have a voltage divider with R1 and R2, R1 input to output & R2 output to ground, the transfer function is R2/(R1 + R2), right? So use the same idea except you now have Z's instead of R's.

What is Z1?
What is Z2?
Then Vo/Vi = Z2/(Z1 + Z2).

It's much easier in this case to use conductance and susceptance instead of resistance and impedance but I'm guessing that would not help you at this stage.

 

[vela]

Anyway so what I did was as follows (using my attached equivalent drawing (2):

loop 1) Vi (s) = [I1(s) . R1] + [I1(s) . R2] - [I2(s) . R1]

loop 2) 0 = [I2(s) . R1] + [I2(s) / sC] - [I1(s) . R1]

I rearranged loop 2 equation to get I2(s) in terms of I1(s) and substituted that into loop 1 equation. I think this would be Vi. As for Vo I assumed that would just be the voltage drop across R2 which is I1(s) . R2.

However, I could not simplify my answer (whatsoever) to what the question gave, making me think that I've done something wrong.

Your work looks fine so far. You're probably just making an algebra mistake when solving for I₁.