My hunch is that this question and your
View attachment 272252 refer to one and the same:
For a function of one variable we write (casually) $$ {df\over dx} = f'\ \Rightarrow \ df = f'\, dx $$ or (for small ##\Delta x##) : $$\Delta f \approx f'\,\Delta x$$
In the case of two variables this becomes $$df = {\partial f\over \partial x} dx + {\partial f\over \partial y} dy$$leading to (C.14) in your image for the case ##f = {x\over y}##.
In your post #1, however, you write $$ g = 4\pi^2\, {L\over T^2} $$$$ {dg\over g} = {L\over T^2}$$which is something else and simply wrong (effectively, it says ## g = 4\pi^2##

)
Could it be you meant $$ {dg\over g} = { d\,{L\over T^2} \over {L\over T^2}}\quad ? $$
I suggest you go a step back to the general formula and work out ##\partial g\over \partial L## and ##\partial g\over \partial T## to come to an expression for ##dg##.
Once you fully understand that, we can work out an alternative approach using C.4 (and, as I suppose C.3).
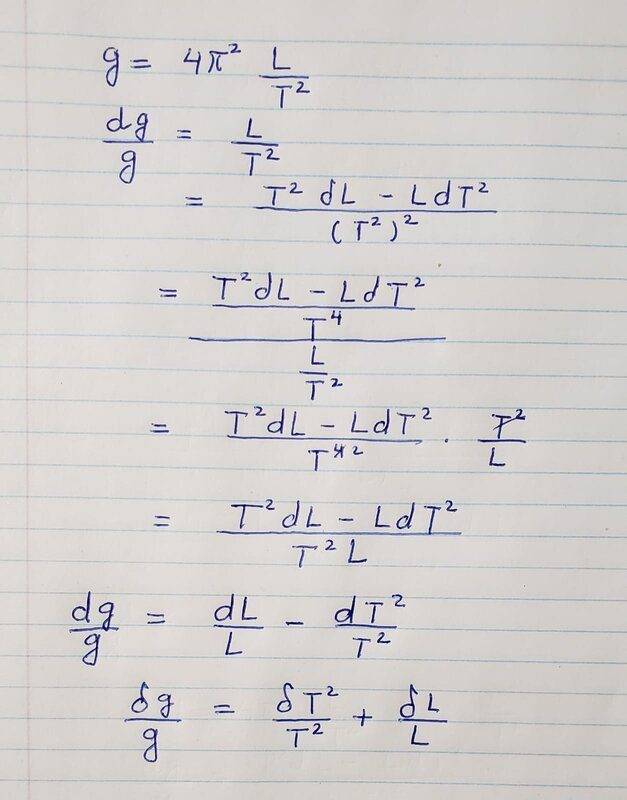
 )
)