Engineering Finding Thevenin's equivalent circuit for AC network

[nicky_2793]

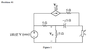
1. Hi everyone, i was given an AC circuit (capture.png) and am required to find the value of the variable resistor Z so that average maximum power is delivered to it.
To solve this i am trying to find the thevenin equivalent circuit but i am stuck and unable to figure it out. Any help would be much appreciated

Homework Equations

Rth=Vth/Eth

The Attempt at a Solution

I think i need to use nodal analysis, KVL and KCL to find Vth
then find short circuit current across Vth in order to get Rth = Vth/Isc

 

[gneill]

Finding the Thevenin equivalent of a network with controlled sources is not always simply a matter of finding the open circuit impedance and voltage in the usual fashion -- the controlled sources can make the impedance vary with the load conditions.

In such cases one way to proceed is to replace the load (Z_o) with a voltage source (introducing a new variable, say v_o). The Thevenin impedance will be given by the ratio of the voltage v_o to the current that it drives into the circuit (be careful with the current direction -- the impedance definition assumes that the current is flowing out of the voltage source and into the circuit).

For this circuit I would be tempted to write KVL mesh equations for the bottom two loops assuming that the current in the top loop is already "solved" since that loop's mesh current is determined by the controlled source which is strictly dependent upon the other two mesh currents that flow through the inductive impedance (in other words, if i3 is the top loop's mesh current, then you replace i3 with i3 = (i1 - i2)*(j5Ω)*(1/10)[A] where i3 would appear in the two bottom loop equations. The resulting expression must have units of Amps [A], so adjust as required).

After solving for the current in the loop containing the load resistance you can use it to write a suitable expression for the power delivered to the load. Maximize this relationship with respect to the load resistance (a touch of calculus).

The algebra may not be pretty...