Finding time period and minimum length of threads

[Saitama]

Homework Statement

(see attachment)
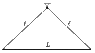
An iron rod of length L is hung at a common point with threads of length \ell which are attached to the two ends of the rod. The rod is displaced a bit in the plane of the threads. What is the length of the threads if the period of the swinging of the rod is the least, and what is this period?

Homework Equations

The Attempt at a Solution

The CM of the rod will perform oscillations similar to a pendulum. Therefore, the time period of oscillation is:
T=2 \pi \sqrt{\frac{l'}{g}}
where l' is the distance of the CM of rod from the hinged point.
l'=\sqrt{l^2-\frac{L^2}{4}}
Substituting this relation in the previous equation and differentiating the result to find the minimum time period doesn't give me the right answer.

Any help is appreciated. Thanks!

 

[voko]

You would have this period if the entire mass were concentrated in the middle of the rod. Which is not the case, so you have to take the moment of inertia into account.

 

[Saitama]

You would have this period if the entire mass were concentrated in the middle of the rod. Which is not the case, so you have to take the moment of inertia into account.

Ah, completely forgot about it. Thanks a lot voko! That solved the problem.