- #1
shanepitts
- 84
- 1
The problem, relevant equations, and my attempt at a solution are all shown on both attached images.
Not sure where the π and and extra (1/4)1/2 is coming from.
Also, I noticed that my final result, in the attemp at a solution should be t=(mb3/4k)1/2, no negative sign.
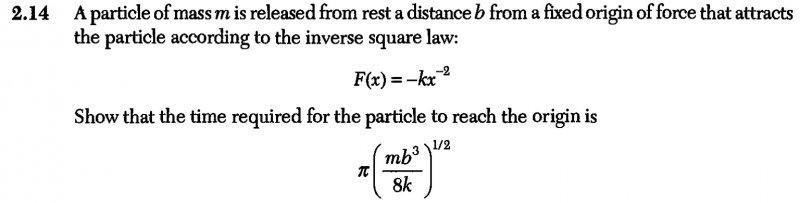
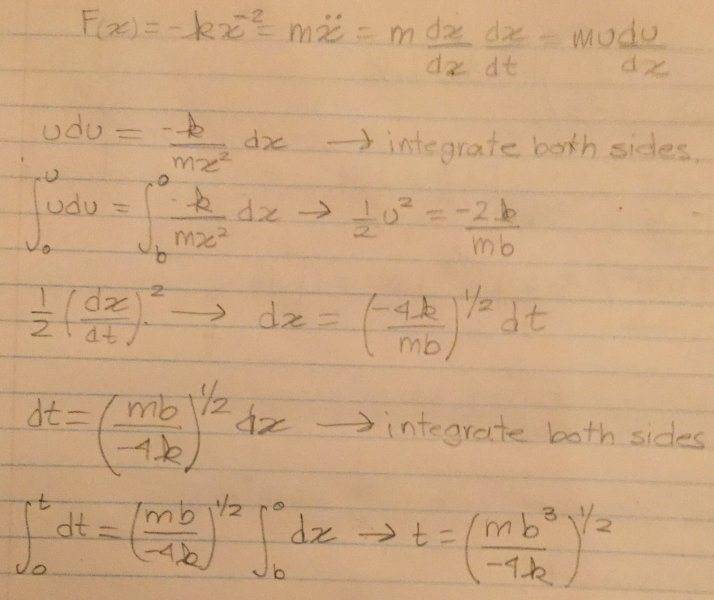
Not sure where the π and and extra (1/4)1/2 is coming from.
Also, I noticed that my final result, in the attemp at a solution should be t=(mb3/4k)1/2, no negative sign.
Last edited: