Finding Vth from Thevenin Equivalent of Circuit

[GBA13]

Homework Statement

Hello everyone!

I am attempting to find the thevenin equivalent for a circuit. I've got the Rth but am not struggling to find the Vth

Homework Equations

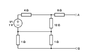
I have included a screen shot of the circuit

The Attempt at a Solution

I thought the best way to go about it was to divide the circuit up into three loops and make three equations.

I got
(1) 1 - 4I1 - 12(I1 - I3) =0
(2) I2 - 1(I2 - I3) = 0
(3) (I3 - I2) - 12(I3 -I1) - 5I3 = 0

If I solve these equations I get I1 = 1/16 A and I2 = 3/4 A so I am thinking that I can add up the two Is to give 13/16 A as the total current in the circuit. But I'm not sure how I can make a find loop which includes both AB and the voltage source to give me Vth.

Could anyone offer a hand?

Thanks very much.

 

[gneill]

Vth is an open-circuit value, so terminals A-B are open. In that case I see only two loops.

However, there's a simpler way to find Vth here. What can you say about how the two 1 Ω resistors are connected?

 

[GBA13]

Vth is an open-circuit value, so terminals A-B are open. In that case I see only two loops.

However, there's a simpler way to find Vth here. What can you say about how the two 1 Ω resistors are connected?

Oh, so are you saying that the path that goes through 3 resistors and AB isn't actually a loop as it isn't closed?

I'm pretty sure the two 1ohm resistors are in parallel, as they share the same nodes.

 

[gneill]

Oh, so are you saying that the path that goes through 3 resistors and AB isn't actually a loop as it isn't closed?

Right. A loop must be a closed path.

I'm pretty sure the two 1ohm resistors are in parallel, as they share the same nodes.

Correct. Does that suggest anything to you?

 

[GBA13]

So that closes up the loops so there's only one loop so I can easily find the current flowing in the circuit using Kirchoff's voltage law. So the current I got was 1/16 Amps. So then I think I need to find a loop which passes through the voltage source and AB so I can rearrange to the find the voltage across AB, but if, like you said, there is only one loop and it doesn't include AB how can I do that?
Thanks for your help, you've been really useful so far.

 

[gneill]

You can sum potential changes between two points without there being a closed loop. So long as you know the potential change across each component on the path between two points in a circuit you can determine the potential difference between those points.

So, what's a path that will take you from B to A? Keep in mind that you've turned the two 1 Ω resistors into a single resistance.

 

[GBA13]

Oh OK, that makes more sense.

So I would start at B and then through the 0.5 ohm resistor made by the two 1 ohm resistors. Then it gets a bit more complicated. I would assume that as the 12 ohm resistor is in parallel with the 1V supply and the 4 ohm resistor, it have the same voltage going across it as the supple and 4 omh resistor combined so doesn't matter which route I take? If that's true then I just go up either one of them and then through last resistor to A.

 

[gneill]

Right. Any path you take from B to A will yield the same result.

 

[GBA13]

Great, thanks very much! I've got it from here.

Thanks very much for all your help! :)