CogitoEAS
- 9
- 0
Finding the charge on each capacitor in series
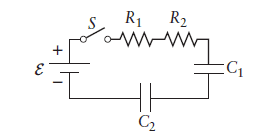
In the circuit in the figure below, assume the resistance values are R1=1,400Ω and R2=2,500Ω, C1=55μF and C2=15μF, and the emf=5.5 V. The switch is labeled S.
Consider the circuit in the figure below and assume the switch has been closed for a very long time.
What are the charges on the two capacitors?
C=Q/V, Loop Rule - 5.5-(Q1/55e-6)-(Q2/15e-6)=0, 1/Ceq=(1/C1)+(1/C2)
I think I'm just blanking on something here because it's either a matter of finding the potential across each capacitor or finding another equation relating Q1 and Q2 so that I can solve for both. Maybe Qtotal=CV(1-e^(-t/tau))=Q1+Q2?
Homework Statement
In the circuit in the figure below, assume the resistance values are R1=1,400Ω and R2=2,500Ω, C1=55μF and C2=15μF, and the emf=5.5 V. The switch is labeled S.
Consider the circuit in the figure below and assume the switch has been closed for a very long time.
What are the charges on the two capacitors?
Homework Equations
C=Q/V, Loop Rule - 5.5-(Q1/55e-6)-(Q2/15e-6)=0, 1/Ceq=(1/C1)+(1/C2)
The Attempt at a Solution
I think I'm just blanking on something here because it's either a matter of finding the potential across each capacitor or finding another equation relating Q1 and Q2 so that I can solve for both. Maybe Qtotal=CV(1-e^(-t/tau))=Q1+Q2?
Last edited: