First Law of Thermodynamics (Eint = Q-W) question. I am only stuck on part (d)

AI Thread Summary
The discussion revolves around solving a thermodynamics problem using the First Law of Thermodynamics, specifically focusing on the calculation of heat (Q) and work (W) in various paths between states. The user has successfully calculated values for parts (a), (b), and (c) but is struggling with part (d), which requires finding Q for path ib given Eint,b = 27 cal. It is noted that the work from state i to b is equivalent to the work from state i to b to f, where the work from b to f is zero due to constant volume. The final guidance suggests using this relationship to determine Q for path ib.
zag4life
Messages
2
Reaction score
0
When a system is taken from state i to state f along path iaf in the figure, Q = 60 cal and W = 10 cal. Along path ibf, Q = 65 cal.
hrw7_18-41.gif

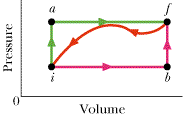
(a) What is W along path ibf? (b) If W = -19 cal for the return path fi, what is Q for this path? (c) If Eint,i = 11 cal, what is Eint,f?(d) If Eint,b = 27 cal what is Q for path ib?(e) For the same value of Eint,b, what is Q for path bf?

Homework Equations


Eint= internal energy of the system; Q= heat; W= work
I have used Eint= Q - W to solve most of the problem.

The Attempt at a Solution


I only am marked wrong on part d which is very frustrating. So far I have:
(a)Wibf = 15 cal because W= Q-E (b) Qfi= -69 cal because Q= -(E)+W (c) Eint,f= 61 cal because Eint,f= Eint+Ei (d) Qib= ? (e) Qbf= 34 because Eint,f =E-Eint,b
Any thoughts?
 
Last edited:
Physics news on Phys.org
Hi, zag4life. Welcome to PF.

How does the work for i \rightarrowb compare to the work for i\rightarrowb\rightarrowf?
 
Well, from b to f, because the volume does not change, work is equal to zero. The work for i,b,f would be the same as the work for i,b I think.
 
Good. So, use that to get Q for ib.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Thermodynamics-work, heat, & internal energy
Replies
1
Views
17K
Making sense of sequence of ideas in MIT OCW's 8.02 notes on Faraday
Replies
1
Views
1K
Why is the work done considered negative in this thermodynamics problem?
Replies
3
Views
1K
Help with this Law of Thermodynamics question please
Replies
27
Views
2K
How Do You Calculate Heat Transfer in a Thermodynamics Piston Problem?
Replies
5
Views
3K
Thermodynamics - cyclic pressure/volume process
Replies
2
Views
13K
The First Law of Thermodynamics
Replies
4
Views
3K
Thermodynamics First Law Question
Replies
4
Views
3K
Thermodynamics: Insulated Box Partition Question
Replies
3
Views
3K
Is Internal Energy Change Consistent for Different Paths in Thermodynamics?
Replies
5
Views
3K

Hot Threads

Recent Insights

Back
Top