maxxlr8
- 12
- 0
A few months back my colleagues and I are facing a problem where the intensity of our sapphire peak fluctuates every time an XRD phase analysis was done, even when the scan was done on the same sample.
By accident, I found that the orientation of the sapphire substrate with respect to phi axis somehow plays a part in the situation.
So, I decided to do a scan following the procedure below:
Below is the result:
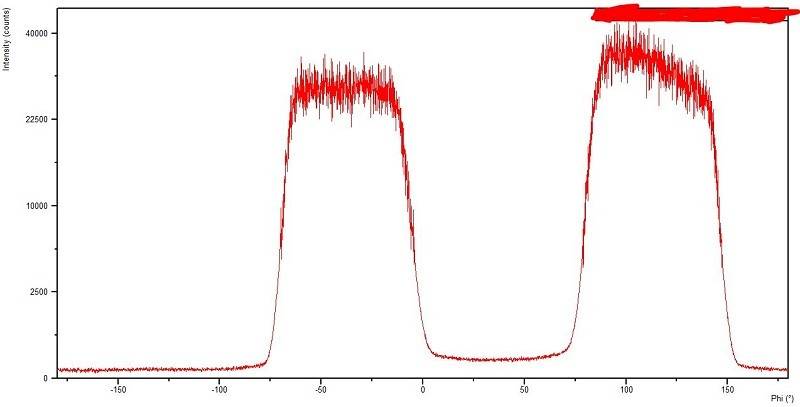
It can be seen that although 2-theta has been placed at the diffraction angle of the sapphire substrate, diffraction only occurs at two main regions in phi, which are approximately:
For now, only samples with sapphire substrates have this kind of problem. It is not known if other samples involving silicon or GaAs substrates have the same issue.
Can anyone help explain the theory behind this observation?
Thank you
By accident, I found that the orientation of the sapphire substrate with respect to phi axis somehow plays a part in the situation.
So, I decided to do a scan following the procedure below:
- Moved the 2-theta to the diffraction angle of (30-30) plane of my sapphire substrate, which is ~68.3 degrees
- As this is a symmetric scan, omega has been rotated to ~34.2 degrees
- Shutter was opened, and the phi axis has been rotated 360 degrees
Below is the result:
It can be seen that although 2-theta has been placed at the diffraction angle of the sapphire substrate, diffraction only occurs at two main regions in phi, which are approximately:
- -63 to -12 degrees
- 85 to 140 degrees
For now, only samples with sapphire substrates have this kind of problem. It is not known if other samples involving silicon or GaAs substrates have the same issue.
Can anyone help explain the theory behind this observation?
Thank you