Fluid flow acceleration in a channel

In summary, the channel has a gradually converging cross-section area. There is a locally flat velocity profile.
  • #1
Proletario
5
0
MODERATOR NOTE: THIS HOMEWORK WAS SUBMITTED TO A NON-HOMEWORK FORUM SO THERE IS NO TEMPLATE

Hi everyone,

I'm stuck on a fluid mechanics problem and maybe you could help me.

As shown in figure, there is a two-dimensional converging channel, in which cross-section area varies linearly with x. If Q is the discharge, determine the flow acceleration along the x-axis (A1, A2 and L are known).
6119a243-1265-4e02-b2cd-6078d0bd7c5a.jpe


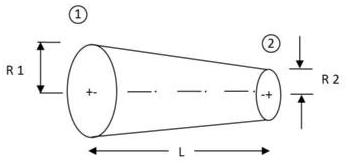
I got for area: A(x)=(A2-A1/L).x+A1

I'm not sure what to do about Q, should Q=A.v be used? Any hint about how to get the velocity field?

Thanks in advance!
 
Last edited by a moderator:
Physics news on Phys.org
  • #2
You don't have any other indication about what they want you to use for discharge? That's an ambiguous term.
 
  • #3
At steady state, the acceleration is vdv/dx. Are you familiar with this term in the momentum balance equations?

Chet
 
  • #4
Chestermiller said:
At steady state, the acceleration is vdv/dx. Are you familiar with this term in the momentum balance equations?

Chet

Do you mean Navier-Stokes eq.? I still don't know how to get the velocity field... :frown:
 
  • #5
boneh3ad said:
You don't have any other indication about what they want you to use for discharge? That's an ambiguous term.

No, that's all the information. I think discharge here means volume per time. That's why I tried to use Q=A.v
 
  • #6
Proletario said:
Do you mean Navier-Stokes eq.? I still don't know how to get the velocity field... :frown:
What about getting v(x) from the two equations in your original post:
A(x)=(A2-A1/L).x+A1
and
Q=A.v

Chet
 
  • #7
Chestermiller said:
What about getting v(x) from the two equations in your original post:
A(x)=(A2-A1/L).x+A1
and
Q=A.v

Chet

I thought the same, but isn't v the mean velocity? If I can use v as the v-field, then the acceleration is quite simple via material derivative.
 
  • #8
Proletario said:
I thought the same, but isn't v the mean velocity? If I can use v as the v-field, then the acceleration is quite simple via material derivative.
It's pretty safe to say that this is what they expected you to do. They just forgot to mention that the channel is converging very gradually and that locally you can assume a flat velocity profile.

Chet
 
  • #9
Chestermiller said:
It's pretty safe to say that this is what they expected you to do. They just forgot to mention that the channel is converging very gradually and that locally you can assume a flat velocity profile.

Chet

Wow, so obvious. Thanks Chet. :bow:
 

Related to Fluid flow acceleration in a channel

What is fluid flow acceleration in a channel?

Fluid flow acceleration in a channel refers to the increase in velocity of a fluid as it moves through a confined space, such as a pipe or channel. This acceleration is caused by a decrease in the cross-sectional area of the channel, which results in an increase in the fluid's velocity in order to maintain the same flow rate.

What factors influence fluid flow acceleration in a channel?

The main factors that influence fluid flow acceleration in a channel include the channel's geometry, the fluid's viscosity, and the fluid's density. A smaller channel with a lower viscosity and higher density fluid will result in a greater acceleration of flow. Additionally, the surface roughness of the channel walls and the velocity of the fluid also play a role in fluid flow acceleration.

How is fluid flow acceleration measured?

Fluid flow acceleration can be measured using various techniques such as flow meters, pressure gauges, and velocity probes. These devices measure the flow rate and pressure of the fluid at different points along the channel, which can then be used to calculate the acceleration of the fluid.

What are some real-world applications of fluid flow acceleration in a channel?

Fluid flow acceleration in a channel is a crucial concept in many engineering and scientific fields, including hydraulic systems, aerodynamics, and fluid dynamics. It is used in the design of pipes, pumps, and turbines, as well as in the analysis of blood flow in the human body and air flow in aircraft engines.

How can fluid flow acceleration in a channel be controlled or manipulated?

Fluid flow acceleration in a channel can be controlled and manipulated through various methods such as changing the channel's geometry, using flow control devices, and adjusting the properties of the fluid. These methods can be used to optimize the flow rate and efficiency of the system, as well as to prevent issues such as turbulence and cavitation.

Similar threads

Double experiment: "Falling ball viscometry" and viscous flow in an horizontal pipe
    • Engineering and Comp Sci Homework Help
Replies
31
Views
1K
Fluid flow through branched nozzles
    • Engineering and Comp Sci Homework Help
Replies
9
Views
2K
Calculating Fluid Flow: Help with Q, A1, A2, Delta h, g & C
    • Mechanical Engineering
Replies
2
Views
2K
Tank Change in Flow Process Modeling
    • Engineering and Comp Sci Homework Help
Replies
5
Views
2K
Fluid flow/heat transfer Area dilemma
    • Engineering and Comp Sci Homework Help
Replies
2
Views
4K
Water Flow Through a Pipe w/180° Horizontal Elbow
    • Engineering and Comp Sci Homework Help
Replies
5
Views
1K
Need help with fluid mechanics question
    • Engineering and Comp Sci Homework Help
Replies
4
Views
2K
I Work - Energy Principle Application to Fluid Flow
    • Classical Physics
2
Replies
35
Views
2K
Fluid mechanics and pipe flow questions
    • Engineering and Comp Sci Homework Help
Replies
9
Views
3K
A Why are the Navier-Stokes equations inconsistent in this case?
    • Classical Physics
Replies
18
Views
1K

Hot Threads

Recent Insights

Back
Top