- #1
Mingsliced
- 18
- 0
Homework Statement
This is simply a sanity check concerning the system described and attached. My concerns are detailed within my attempts at the solution. Any guidance will be greatly appreciated!
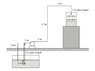
The diagram attached represents a process for which a pump and associated pipe work require to be correctly sized. The liquid is to be pumped from the underground storage vessel which is vented to atmosphere (assume 1 bar pressure) to a pressurised container supported some distance above ground level. The pump is sited at ground level and must be capable of delivering 0.01 m3 s–1 with a maximum velocity of 1.8 m/s–1.
Q = 0.01 m3 s–1
V = 1.8 m/s–1
D = 90 mm = 0.09 m
Liquid density, ρ = 960 kg m–3
Liquid viscosity, μ = 0.081 Pa s
L = 27m (from pump) or 32m (total length).
Homework Equations
See below.
The Attempt at a Solution
Calculate Mean Velocity:
Um = (4 * Q)/(π * D2)
Um = (4 * 0.01)/(π * 0.092)
Um = 1.57 m/s-1
Calculate Reynolds number:
Re = (Um * D * ρ)/μ
Re = (1.57 * 0.09 * 960)/0.081
Re = 1675
As the Reynolds number calculated is less than 2000, the flow is assumed streamlined. Therefore I will use the Poiseuille equation to calculate head loss due to friction:
Hf = (32 * μ * L * Um)/(ρ * G * D2)
Hf = (32 * 0.081 * 32 * 1.57)/(960 * 9.81 * 0.092)
Hf = 1.707 m
The first issue I am having is the length of pipe to use within the Poiseuille equation. If you look at the diagram, you can see that the pipe length from the pump to the container is 27m whilst the total pipe length for the system is 32m. I have used total pipe length but I am not sure whether you just count the pipe length from the pump to the container, especially as the diagram shows a line break. Clarification of this would be great.
The second issue I'm having is finding minor head losses from the 90° pipe bends, entry to the pipe and exit from the pipe. Do I count the entire system or simply the pipework starting at the pump and ending at the container?
Just very minor problems that need clarifying really, thanks!