muhammed_oli
- 10
- 0
Homework Statement
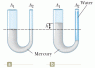
Mercury is poured into a U-tube as shown in Figure a. The left arm of the tube has cross-sectional area A1 of 9.4 cm2, and the right arm has a cross-sectional area A2 of 4.50 cm2. One hundred grams of water are then poured into the right arm as shown in Figure b.
(b) Given that the density of mercury is 13.6 g/cm3, what distance h does the mercury rise in the left arm?
Homework Equations
P=P(o)+ρgh where ρ is density of subject in question
The Attempt at a Solution
Hey everyone, just need a little conceptual help here. I'm unsure how to find the height of the water and the reasoning behind it.
My equation is ρhggh = ρwghw
where hw is the height of water in the tube above the line. The volume displaced is equal, I'm that far but how does the water above the line factor into the calc? Or just set me straight for this, it seems the more I think about it the further I get from an answer, there's something I need to equate conceptually which I am not getting.