Aerospace
- 39
- 0
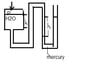
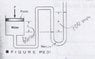
A piston having a cross-sectional area of 0.07 m^2 is located in a cylinder containing water as shown in the figure. An open u-tube manometer is connected to the cylinder as shown. For h1=60 mm and h=100 mm, what is the value of the applied force, P, acting on the piston? The weight of the piston is negligible.
I'm confused because there is more than one "u"-shape in the figure, so, it's unclear to me how to proceed.
Help would be appreciated!
legend for figure :
p = piston
first weird looking h = h1
second weird looking h = h
piston is present on top of the water.
Force P downwards on piston.
I'm confused because there is more than one "u"-shape in the figure, so, it's unclear to me how to proceed.
Help would be appreciated!
legend for figure :
p = piston
first weird looking h = h1
second weird looking h = h
piston is present on top of the water.
Force P downwards on piston.