Fluids and pressure with kinematics

[emag]

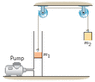
1. There is a cylinder fitted with a piston, the piston has a mass m1 of 0.50 kg and a radius of 2.50 x 10^-2 m. The top of the piston is open to the atmosphere. The pressure underneath the piston is maintained at a reduced (but constant) value by means of the pump. As shown, a rope of negligible mass is attached to the piston and passes over two massless pulleys. The other end of the rope is attached to a block that has a mass of m2 = 9.5 kg. The block falls from rest down through a distance of 1.25 m in 3.30 s. Ignoring friction, find the absolute pressure beneath the piston.

m1 = .5 kg
m2 = 9.5 kg
R = 2.5x10^-2 m

d =1.25 m
T = 3.30s

Homework Equations

P2 = P1 + pgh
P=F/Area
acceleration = V2-V1/T2-T1
F=MA

The Attempt at a Solution

(m1+m2)a-m2*g+m1*g+Patm = P2

didn't work, I tried comparing the amount of force required to oppose the force of gravity in order to make the descending block have an acceleration that matches the calculated acceleration for the falling block. Any help on this problem would be most appreciated, I have a few more stumpers if anyone thinks they know thermodynamics well enough

 

[Hootenanny]

Welcome to the forums,

I can't see your attachment yet (pending approval), but perhaps conservation of energy would be the way to go?

 

[emag]

___________
O O
| |
| |
| m2
|
| | |
| | |
|[m1]|
| |
| ===={pump}

 

[emag]

hmm that didnt come out right... "." represent empty space
...___________
...O .....O
...|... |
...|...|
...|..... m2
...|
|..|...|
|..|...|
|[m1]|
|...|
|...|===={pump}

I would love to use conservation of energy equations but I am unsure of how to implement them in this particular problem

 

[Hootenanny]

Okay, if you don't want to use conservation of energy that's no problem. I think the question is leaning towards kinematics anyway. With respect to your equation;

(m1+m2)a-m2*g+m1*g+Patm = P2

Note that pressure, is not equivalent to force. You have to multiply the the pressure by the area over which it is applied in order to represent the force. Do you follow?

 

[emag]

I tried that but in the end since Patm = F1/A
if you have Patm which I was using 1.013x10^5 you have to multiply that times the area then divide it again by the area in the equation: Patm = f1/a
= Patm*a/a = patm all over again... I even tried setting p2 = F/A and trying it that way but it didnt work, and I am not sure if I am even supposed to be using 1.013x10^5 because it isn't listed in the problem.. I don't think I am supposed to assume anything in this..

 

[Hootenanny]

Atmospheric pressure, it just one of them numbers you are expected to know. So now your equation becomes;

$$P_2A = P_{atm}A + (m_1-m_2)g + (m_2+m_1)a$$

You can determine the acceleration yourself, which only leaves one unknown, P₂.

 

[emag]

but how did you get PatmA and P2A? is that when you substitute F/A for P

 

[Hootenanny]

but how did you get PatmA and P2A? is that when you substitute F/A for P

Correct, from the definition of pressure; $P = F/A \Rightarrow F = PA$.

 

[emag]

Thank you i'll have to wait till monday to see if it works.

 

[Hootenanny]

Thank you i'll have to wait till monday to see if it works.

It was a pleasure, let us know how you get on.