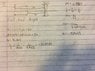PhyHyped
Homework Statement
The distance between an object and its upright image is 28.0 cm. If the magnification is 0.550, what is the focal length of the lens that is being used to form the image?
Homework Equations
1/f = 1/so + 1/si
M= -si/so
The Attempt at a Solution
See included image.
Comments
I've been having a hard time with this all day any help would be amazing.
Can't seem to get the right answer.