Force on a charge on magnetic field

[Genericcoder]

Hi guys,

I am solving some magnetism questions,but somewhat confused about right hand rule.

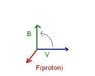
Determine the magnitude and direction of the force on an electron traveling 8.75 * 10^5 m/s horizontally to the east in vertically upward magnetic field of strnegth 0.75T?


We know since this is perpindcular to the magnetic field it will have maximum since sin(90) would be 1,so we can calculate the the force easily.

F = qVBsin;
F = 1.05;

What I don't understand is the direction first I did normally right hand rule,but since that charge is an electron it should be the opposite to what right hand rule gives us.

So I got the direction as South,but my book says west that should be the direction on a given proton not electron right ?

 

[ehild]

You can visualize the direction of the force if you imagine that you rotate v into B (by the angle less than pi). The force points to that direction from where the rotation looks anti-clockwise. To the South for a proton, opposite for the electron, too North. You did something wrong with the right-hand rule. F=q vxB (vector product).

ehild

 

[Genericcoder]

I see I just rechecked I orientated by hand wrong that's why I got wrong answer :S.
Is their a way to check if I got my answer correctly mathematically ?

 

[ehild]

You can find the force from the components of v and B. Do you know the determinant method for calculating a vector product?

ehild

 

[Genericcoder]

No I don't know about it :S could you suggest a tutorial to read about this method?

 

[ehild]

The determinant only makes easier to memorize cross product. (See for example http://mathworld.wolfram.com/CrossProduct.html).

You certainly know that

\vec a\times \vec b=(a_yb_z-a_zb_y) \vec i+(a_zb_x-a_xb_z) \vec j+(a_xb_y-a_yb_x) \vec k.

The force is \vec F= q\left[\vec v \times \vec B\right]. If the x-axis points to East, the y-axis points to North and the z axis point upward, \vec v=v \vec i and \vec B=B \vec k, and \vec F=q v \vec i\times B \vec k=-qvB \vec j.

ehild

 

[Genericcoder]

I see thanks a lot :).