Force on a Pulley: Understanding Tension and Tangents

[user240]

Homework Statement

I'm having trouble understanding an example given in K&K's Intro to Mechanics textbook.

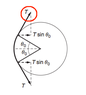
'A string with tension $T$ is deflected through an angle $\theta_0$ by a smooth fixed pulley. What is the force on the pulley'.

I don't understand how (in the first picture) they got the horizontal force from the tension to be $Tsin(\theta_0)$, unless the angle I've circled in red is somehow $\theta_0$ also. In which case, how would you prove that?

I also don't get how (second picture) they found the force from the string tension to be $Tsin(\frac{\Delta\theta}{2})$.

 

[Orodruin]

I don't understand how (in the first picture) they got the horizontal force from the tension to be $Tsin(\theta_0)$, unless the angle I've circled in red is somehow $\theta_0$ also. In which case, how would you prove that?

The string is tangent to the pulley ...

 

[zwierz]

By $\boldsymbol T_1$ denote the tension force from above (in the first picture) and by $\boldsymbol T_2$ denote the tension force from below, $|\boldsymbol T_2|=|\boldsymbol T_1|=T$. Thus the pulley expirences the force $\boldsymbol T_1+\boldsymbol T_2$. This is just a sum of two vectors.

 

[user240]

The string is tangent to the pulley ...

Could you please elaborate? I'm probably overlooking something very basic here but it's not obvious to me why the force from the rope is then given as $2Tsin(\theta)$

By $\boldsymbol T_1$ denote the tension force from above (in the first picture) and by $\boldsymbol T_2$ denote the tension force from below, $|\boldsymbol T_2|=|\boldsymbol T_1|=T$. Thus the pulley expirences the force $\boldsymbol T_1+\boldsymbol T_2$. This is just a sum of two vectors.

I'm not sure why the force happens to be $2Tsin(\theta)$ though.

 

[Carbon123]

The tension is tangential to the pulley (90 degrees ) thus the angle that vector T encloses with the vertical is θ : you can prove this by simple geometry ) the T cos( θ) component cancels out while the only force left is the sum of the two tension pointing inwards.The first image shows the small angle taken to be 2θ and therefore the angle is θ but the second one is considering an angle θ so it becomes θ/2.Both are showing a diffrent magnification on the string.However, if you integrate the force you get the same total force.(but with different limits in the integral ,(for the first one is from 0 to 90while the second one is 0 to 180,which you can prove ,is equivalent)

 

[zwierz]

I'm not sure why the force happens to be 2Tsin(θ)2Tsin(\theta) though.

introduce a coordinate frame and expand the vectors in coordinates

 

[haruspex]

it's not obvious to me why the force from the rope is then given as 2T sin(θ)

You asked two questions, the first re T sin(θ₀₎, the second re T sin(Δθ/2).
Orodruin was answering tne first question. It's simple geometry. The radius makes angle θ₀ to the horizontal. The radius is perpendicular to the tangent. So the tangent makes angle θ₀ to the vertical.

In the second picture, the author considers a short arc of the circle subtending angle Δθ at the centre. She takes a radius in the middle of that and constructs the tangent at that point, as well as tangents at each end of the arc. Can you see that the tangents at the end each make angle Δθ/2 to the tangent in the middle?