PhysicStud01
- 174
- 0
Homework Statement
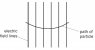
The diagram shows the path of a charged particle through a uniform electric field, having vertical
field lines.
(the iamge has been attached)
What could give a path of this shape?
A a positive charge traveling left to right in a field directed downwards
B a positive charge traveling right to left in a field directed downwards
C a negative charge traveling right to left in a field directed upwards
D a negative charge traveling left to right in a field directed downwards
Homework Equations
The Attempt at a Solution
Ans is D. but i can't understand. it's an electric field. flemming rules don't apply. why is D correct. and the other wrong. shouldn't a -ve charge just move vertically up??