neosocra
- 3
- 0
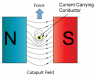
A solenoid, of sufficient length to consider external flux to be zero, passes through a uniform magnetic field with significant length on both ends extending beyond the field.
Will a torque be exerted upon the solenoid ? Or do the windings effectively mask the internal solenoid field from the external? (again, with each solenoid pole well beyond the field; a very long permanent magnet would receive a torque, I'd imagine)
Would the vector orientation of the external uniform field relative to the B vector of the solenoid make any difference?
Will a torque be exerted upon the solenoid ? Or do the windings effectively mask the internal solenoid field from the external? (again, with each solenoid pole well beyond the field; a very long permanent magnet would receive a torque, I'd imagine)
Would the vector orientation of the external uniform field relative to the B vector of the solenoid make any difference?