Force P that will start the block to move

[darkmagic]

1. Homework Statement .

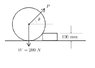
Find the force P and theta that will start the block to move.
The illustration can be found at the attachments.

Given:
W= 200 N
Radius of the circle 400 mm
length of the block 100 mm

The unknowns are the P and theta.

2. Homework Equations .

Summation of Fx=0
Summation of Fy=0

Those are the equations that I see that can be used.

3. The Attempt at a Solution .

Note that there is no normal force between the cylinder and the surface since the system will start to move.

There are three forces acting on the system: the weight (W), force P, and normal force between the block and the cylinder (Nb). The horizontal angle of the Nb can be acquired by using right triangle where hypotenuse equals the radius and and one leg equals radius minus length of the block. By using sine function, the angle can be acquired. There are three unknowns left: P, theta, and Nb. There are only 2 equations that I can see: the summation of horizontal component and the summation of vertical component. What should I do?

Thank you.

 

[Doc Al]

I assume the problem is to find the minimum force P (and the angle it makes) that will start the cylinder going over the step.

Hint: Consider torques.

 

[darkmagic]

yes that is it. I think you cannot use moments in here. How should I start using torques?

 

[Doc Al]

I think you cannot use moments in here. How should I start using torques?

Moments and torques are the same thing. Why can't you use them? (You've got to.)

Consider the torques about the edge of the step. What torque does the weight produce? What torque does force P produce? (At what angle must P act to produce the most torque?)

 

[darkmagic]

so the axis is the point of application of the block and the cylinder? okay i try it.

 

[darkmagic]

I still got no result. My answer becomes 0=0. At that point, Nb has no torque and the W and Py has the same distance which is around 264. and Px has a distance of 300 from the point. When I solved it, I cannot get a result. Why?

 

[Doc Al]

I'm not quite sure what you're doing. Forget Px and Py, just consider P. What angle must it make to maximize the torque it produces? (What angle must the P vector make with the line from the corner of the step to the center of the cylinder?) Then find the minimum value of P such that its torque is just enough to overcome the torque due to the weight of the cylinder.

 

[darkmagic]

Do you mean step as the corner of the block? I got Nb about 50. I think I'm wrong. Do you mean that torque of P equals torque of W?

 

[Doc Al]

Do you mean step as the corner of the block?

Yes. The cylinder will pivot about the corner of the block/step. Calculate torques about that point.

Do you mean that torque of P equals torque of W?

Yes.

 

[darkmagic]

My problem now is the angle. I cannot combine sin theta and cosine theta. The equation is like: sin theta = 1-cos theta. Can I substitute square root of 1 - cos square theta to sin theta to get the angle. What other methods can I use?

 

[Doc Al]

My problem now is the angle. I cannot combine sin theta and cosine theta. The equation is like: sin theta = 1-cos theta. Can I substitute square root of 1 - cos square theta to sin theta to get the angle. What other methods can I use?

I don't understand what you are doing. Answer the two questions I asked in post #7.

 

[darkmagic]

Now I have P, I cannot get the angle. Can you give me another hint?

 

[Doc Al]

Now I have P, I cannot get the angle. Can you give me another hint?

I'm still waiting for you to answer my questions from post #7. (In order to find P, you must have the angle it makes with the radius.)

 

[darkmagic]

I have P but no angle. My equations are Pcos theta = 0.66R and Psin theta = 200 - 0.75R. I cannot really get it. There are two unknowns now but I still cannot get it. The P I get is about 130. When I substitute I cannot get R or theta.

 

[Doc Al]

I have P but no angle. My equations are Pcos theta = 0.66R and Psin theta = 200 - 0.75R. I cannot really get it. There are two unknowns now but I still cannot get it. The P I get is about 130. When I substitute I cannot get R or theta.

I'm going to quote myself:

I'm not quite sure what you're doing. Forget Px and Py, just consider P. What angle must it make to maximize the torque it produces? (What angle must the P vector make with the line from the corner of the step to the center of the cylinder?) Then find the minimum value of P such that its torque is just enough to overcome the torque due to the weight of the cylinder.

Please answer the two questions I ask. (It's really just one question, restated.)

When you answer those questions, you'll have the angle. Then you can find P using one simple torque equation.

 

[darkmagic]

Up to this day, it is still negative. However, I will try to figure it out. I have 1 week remaining. Ok. Thank you.

 

[Doc Al]

Up to this day, it is still negative.

Let me ask you this. If you wanted to turn a wrench with maximum torque, which direction would you push or pull? (See: http://hyperphysics.phy-astr.gsu.edu/hbase/torq.html" )

 

[darkmagic]

I think I know now. The force P should be perpendicular to the step. If the angle of the normal between block and cylinder is 30, then the theta will be 60. Am I right?

 

[Doc Al]

The force P should be perpendicular to the step.

It should be perpendicular to the line from the edge of the step to the center of the cylinder.

If the angle of the normal between block and cylinder is 30, then the theta will be 60. Am I right?

I'm not sure how you are defining your angles.

 

[darkmagic]

The normal is also directed to the center of cylinder.

 

[Doc Al]

The normal is also directed to the center of cylinder.

True. So I think I see what you're saying: If the normal makes an angle of 30 with the horizontal, then theta will equal 60 degrees. Yes!

 

[darkmagic]

Ok. thank you. I will solve it. How about if the statement only says find theta and P without the minimum, can you solve it? By the way, do you have any application of Bernoulli's differential equation. It is one of my threads. I need at least three