rdijulio
- 3
- 0
Summary: Looking of someone to double check my work on this design issue.
I am posting this here because I am no longer a student, but it is similar to a simple homework problem
Problem: I am designing a rubber-band like product for a client. He wants to take a durable rubber band and stretch it over a circle that is 9.875" diameter and 1.75" wide. He wants it to be easily installed and removed, enough for a child or elderly person of 70 years. So I estimated 10 lbs of force would be ideal. The question I am trying to solve is: (At what un-stretched diameter is 10 lbs of force required to stretch this band to 9.875")
Relevant Equations: F =( [Ln-Lo]/Lo) * E * A
A=Cross Sectional Area (The band is not a rectangle)
E=Elastic Modulus
Ln=Length New (9.875"*π - 31.023" or .78798m)
Lo=Variable
F=Force (10lbs or 44.5N)
This is just Hooke's law, and I know that elastic bands don't behave under hooke's law at a certain point, but this was the best approximation I could find. Solving for Lo gives you:
Lo=Ln/(1 + (F / (E*A) ) )
The material I chose to calculate is Silicone 60A Durometer. I pulled the elastic modulus from this graph:
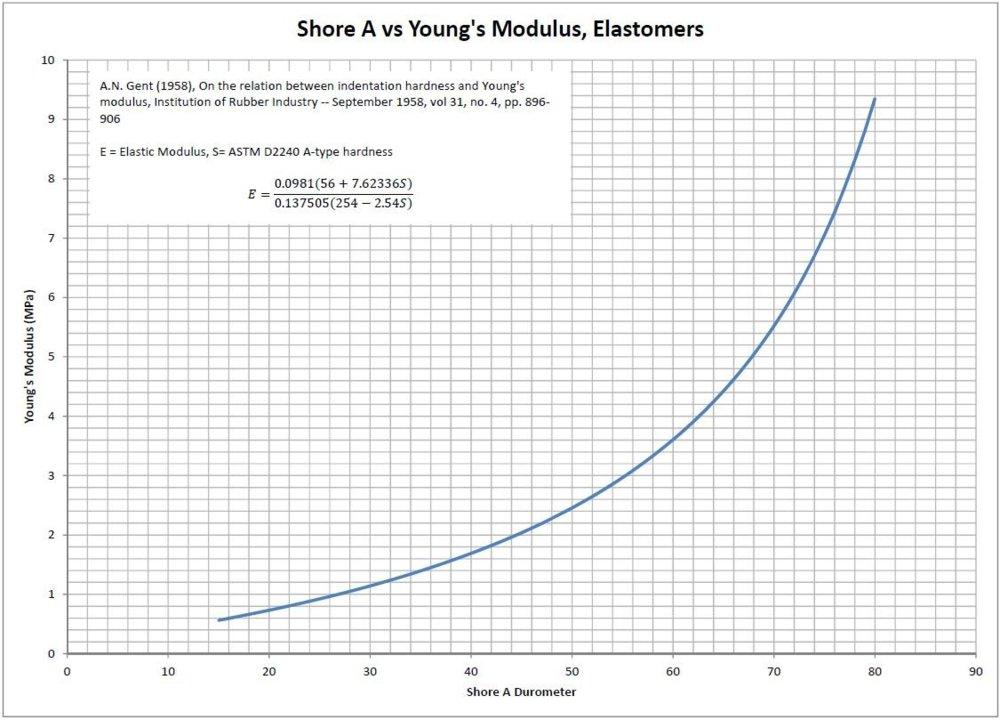
Which gives me an E=3.6e6 pa.
The next step was to calculate the cross sectional area: Here is the drawing with the equations and variables:
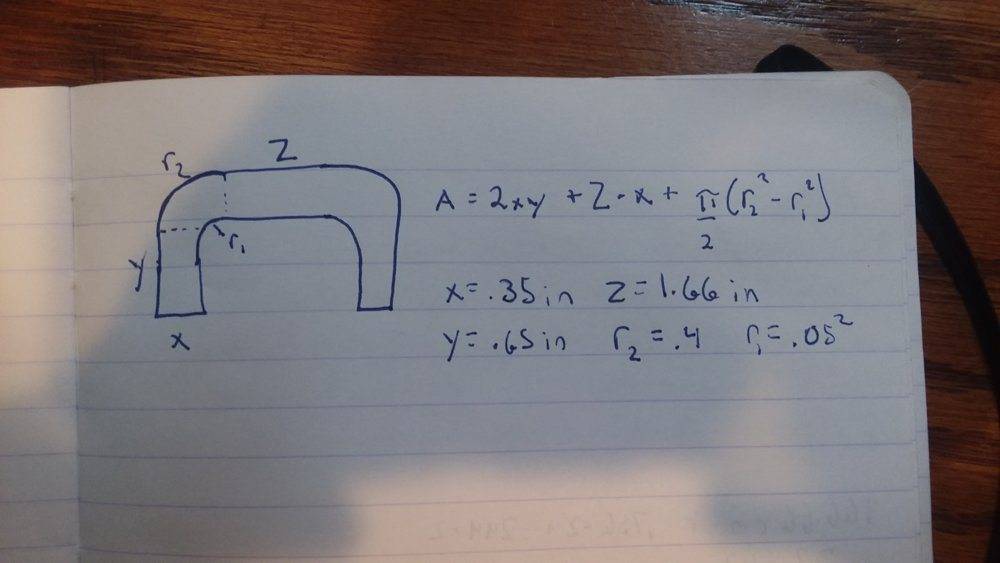
Plugging in gives 1.2834in2 or 8.28e-4m2
Now we have all our values:
Lo = .78798 / (1 + 44.5 / (3.6e6*8.28e-4) ) = .77638
D = .77638/pi = .2471m or 9.72inchesJust looking for someone to check my work. Provide possibly any more feedback, or an alternative way to calculate what I need. Thanks!
I am posting this here because I am no longer a student, but it is similar to a simple homework problem
Problem: I am designing a rubber-band like product for a client. He wants to take a durable rubber band and stretch it over a circle that is 9.875" diameter and 1.75" wide. He wants it to be easily installed and removed, enough for a child or elderly person of 70 years. So I estimated 10 lbs of force would be ideal. The question I am trying to solve is: (At what un-stretched diameter is 10 lbs of force required to stretch this band to 9.875")
Relevant Equations: F =( [Ln-Lo]/Lo) * E * A
A=Cross Sectional Area (The band is not a rectangle)
E=Elastic Modulus
Ln=Length New (9.875"*π - 31.023" or .78798m)
Lo=Variable
F=Force (10lbs or 44.5N)
This is just Hooke's law, and I know that elastic bands don't behave under hooke's law at a certain point, but this was the best approximation I could find. Solving for Lo gives you:
Lo=Ln/(1 + (F / (E*A) ) )
The material I chose to calculate is Silicone 60A Durometer. I pulled the elastic modulus from this graph:
Which gives me an E=3.6e6 pa.
The next step was to calculate the cross sectional area: Here is the drawing with the equations and variables:
Plugging in gives 1.2834in2 or 8.28e-4m2
Now we have all our values:
Lo = .78798 / (1 + 44.5 / (3.6e6*8.28e-4) ) = .77638
D = .77638/pi = .2471m or 9.72inchesJust looking for someone to check my work. Provide possibly any more feedback, or an alternative way to calculate what I need. Thanks!