klopez
- 21
- 0
[SOLVED] Forces, Acceleration...Hard Stuff (HELP!)
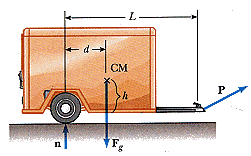
A trailer with loaded weight Fg is being pulled by a vehicle with a force P. The trailer is loaded such that its center of mass is located as shown. Neglect the force of rolling friction and let a represent the x component of the acceleration of the trailer.
(a) Find the vertical component of P in terms of the given parameters. (Use F_g for Fg, a, d, L, h, and g as appropriate in your equation.)
I have no idea on how to use come up with an expression that involves acceleration. In matter of fact I do not know where to start because this looks confusing. Can anyone give me advice?
Thanks,
Kevin
A trailer with loaded weight Fg is being pulled by a vehicle with a force P. The trailer is loaded such that its center of mass is located as shown. Neglect the force of rolling friction and let a represent the x component of the acceleration of the trailer.
(a) Find the vertical component of P in terms of the given parameters. (Use F_g for Fg, a, d, L, h, and g as appropriate in your equation.)
I have no idea on how to use come up with an expression that involves acceleration. In matter of fact I do not know where to start because this looks confusing. Can anyone give me advice?
Thanks,
Kevin