Saad
- 18
- 0
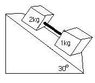
Two boxes, m1 = 1.0kg with a coefficient of kinetic friction of 0.10, and m2 = 2.0kg with a coeffeicient of kinetic friction of 0.20, are placed on an inclined plane inclined at 30 degrees with the horizontal. If a taut string is connected to the blocks, then what acceleration does each block experience?
Note: Free body diagrams should be useful.
Note: Free body diagrams should be useful.