shawli
- 77
- 0
Homework Statement
A rope exerts a force of magnitude of 21 N, at an angle 31 degrees above the horizontal, on a box at rest on a horizontal floor. The coefficients of friction between the box and the floor are s=0.55 and k=0.50 . The box remains at rest. Determine the smallest possible mass of the box.
Homework Equations
Fs= s*Fnormal , Fk=k*Fnormal
F=ma
The Attempt at a Solution
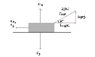
I've attached my system diagram to the post.
Using vector components, I find that Fapp-x=18 N and Fapp-y=10.8N. That's all I know how to do here :/.
I have to solve for mass, but I'm not sure how the physics is working. Can someone start me off on how to solve this question?