Forces in a Line: Examining the Relationship Between Mass and Force

  • Thread starter Thread starter Heexit
  • Start date Start date
  • Tags Tags
    Forces Line
Click For Summary
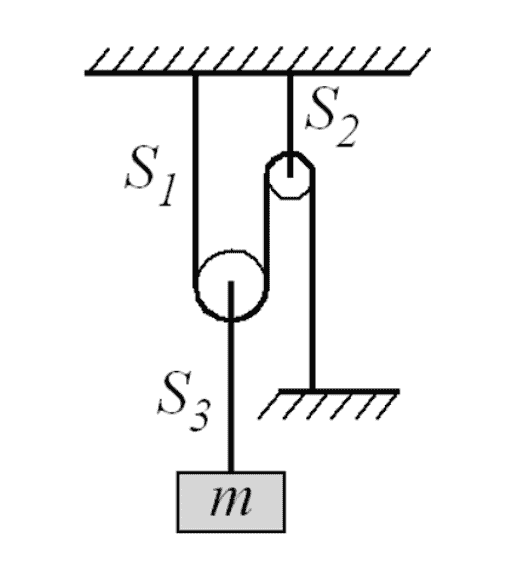
The discussion revolves around the relationship between mass and force, specifically questioning whether S1 equals mg/2 in a given scenario. Participants analyze the forces acting on the system, focusing on the implications of mass distribution and gravitational force. The reasoning includes examining the equilibrium of forces and the application of Newton's laws. Clarifications on the correct interpretation of the forces involved are provided to support the argument. The conversation emphasizes the importance of understanding fundamental physics principles to solve such problems accurately.
Heexit
Messages
10
Reaction score
3
Thread moved from the technical forums to the schoolwork forums
Hello!
1679570465759.png

In the following image, is it true that S1 = mg/2.
Thanks for answears!
 
Physics news on Phys.org
Thread 'Chain falling out of a horizontal tube onto a table'

Thread 'Chain falling out of a horizontal tube onto a table'

My attempt: Initial total M.E = PE of hanging part + PE of part of chain in the tube. I've considered the table as to be at zero of PE. PE of hanging part = ##\frac{1}{2} \frac{m}{l}gh^{2}##. PE of part in the tube = ##\frac{m}{l}(l - h)gh##. Final ME = ##\frac{1}{2}\frac{m}{l}gh^{2}## + ##\frac{1}{2}\frac{m}{l}hv^{2}##. Since Initial ME = Final ME. Therefore, ##\frac{1}{2}\frac{m}{l}hv^{2}## = ##\frac{m}{l}(l-h)gh##. Solving this gives: ## v = \sqrt{2g(l-h)}##. But the answer in the book...
View full post »

Similar threads

Forces for bodies connected by a wire on inclined surface
Replies
4
Views
1K
Calculating acceleration of a prism and block connected to a wall through a rope and pulley
Replies
4
Views
527
A cylinder connected to a hanging mass
Replies
21
Views
585
Exploring the Relationship between Buoyancy Force and Gravitational Force
Replies
5
Views
1K
Angle between normal force and radial line for cylindrical coordinates
Replies
21
Views
2K
Relation between Friction, Velocity, and Acceleration
Replies
16
Views
1K
Tangent Angles for Lines of Force, Two Equal Positive Charges
Replies
29
Views
1K
What minimum speed do we need to give a charged ball?
Replies
12
Views
1K
Struggling to make relation between elastic force and height
Replies
11
Views
378
Does levitation distance increase as Fg increase???
Replies
1
Views
949