Forces on systems in equilibrium

[ebola_virus]

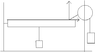
set up two retort stands to support a pulley and a pivot and arrange the apparatus as shown in the diagram attached... and I'm kinda stuck as to how to find the mass of the beam in this instance?

Could you give me any starting references i can work along with; torque is involved, but i just don't undersatnd because I was thinking that the involvement of the pulley is quite important?

 

[sporkstorms]

The first step in a problem like this is always: draw a diagram (done), and label all the forces with vectors [arrows].

So label the forces first (tensions on strings, forces of gravity, etc). Then, we know the system is in equilibrium, which means the net force is zero. That is, all the forces will cancel each other out.

This allows you to start writing relationships between the variuos forces.