robertjford80
- 388
- 0
Homework Statement
The Attempt at a Solution
I don't understand where that 2 comes from in the denominator in cos nπ/2
robertjford80 said:Homework Statement
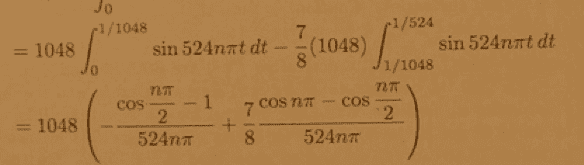
The Attempt at a Solution
I don't understand where that 2 comes from in the denominator in cos nπ/2
robertjford80 said:of course i always do my own derivation. my own derivation is -cosnπ/524nπ - 1/524nπ
There, I'm still as clueless I was before.