You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
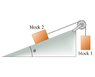
Free-body diagram for two boxes connected on a pulley.
AI Thread Summary
In a frictionless environment with two boxes connected by a pulley, the discussion centers on identifying actual forces for a free-body diagram. Participants clarify that "actual" forces are those with identifiable agents, such as gravity, normal force, and tension from the rope. It is emphasized that "ma" is not a force but rather the result of Newton's second law, which should not be included in the diagram. The correct approach involves identifying all forces acting on each block, with gravity and tension being the primary forces for both blocks. Understanding how to represent forces in the context of Newton's laws is crucial for accurately drawing free-body diagrams.
Physics news on Phys.org
Doc Al
Mentor
- 45,578
- 2,436
A free body diagram should only show the actual forces acting on the body. Is "ma" a force?
ysk1
- 32
- 1
ma equals F, so I'd say ma is a force. Am I wrong?
What do you mean by saying "actual" forces?
Could you please tell me what actual forces are?
How can I know if a force is an actual force or not?
Thank you.
What do you mean by saying "actual" forces?
Could you please tell me what actual forces are?
How can I know if a force is an actual force or not?
Thank you.
paque
- 4
- 0
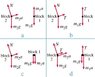
Well the way that i'd work on this problem is by identifyiing every force acting upon each blockysk1 said:ma equals F, so I'd say ma is a force. Am I wrong?
What do you mean by saying "actual" forces?
Could you please tell me what actual forces are?
How can I know if a force is an actual force or not?
Thank you.
Upon Block Block two, i'd say that there are 3 forces acting upon the block (3/4 of the possibilities agree with me, a,b and c)
These forces are :
Gravity - one would hope that we are on the earth... and that the Earth pulls down...
Force normal - else the block is so havy that it just goes crashing through the table
The pull of the other block via tension on the string- it pulls the other way.
I believe answer D is incorrect due to the fact that the string is already pulling on it w/ T, and that there is no other means for block one to affect block two,
So have to two forces pull in the same direction that block one pulls, can't happen as there is really only one object pulling rightwards/downwards/clockwise
Now, regarding the other block, block one, i'd say that there are just two forces acting on it, one upwards, and one downwards. (2 of the answers agree with me,a and b, the other two contradicting each other)
Gravity, and the string, again
Now i believe that tensionis a better term to use versus accelaration*mass, because, though M1a is a potentially valid label, it isn't conclusive, as you would still need to find the tension to solve for "a". On the other hand, tension can be found by determining the blocks' pull on the string, i.e. m1g, m2gx
(two of the responses agree with me,b and d, the other two contradicting each other)
the common answer throughout that i concur with is b.
Last edited:
ysk1
- 32
- 1
But I still don't get one thing: what forces to include in free-body diagram in presence of forces displaying Newton's 3rd law.
A system constituting Newton's 1st or 2nd law is not difficult to draw free-body diagram, but how do you know what forces to include when forces constituting Newton's 3rd law also exist in the system?
A system constituting Newton's 1st or 2nd law is not difficult to draw free-body diagram, but how do you know what forces to include when forces constituting Newton's 3rd law also exist in the system?
Last edited:
Doc Al
Mentor
- 45,578
- 2,436
By "actual" forces, I mean forces that have an identifiable agent--where something is actually pulling or pushing. The tension from the rope is exerted by the rope, gravity is exerted by the earth, the normal force is exerted by the surface. The only "long range" force in the mix is that of gravity; all the other forces are "contact" forces--something (like a rope or a surface) actually touches the object in order to produce a force on it.ysk1 said:ma equals F, so I'd say ma is a force. Am I wrong?
What do you mean by saying "actual" forces?
Could you please tell me what actual forces are?
How can I know if a force is an actual force or not?
"ma" is not a force. The net force on an object equals "ma", due to Newton's 2nd law. But don't show "ma" on a free body diagram!
Kindly see the attached pdf. My attempt to solve it, is in it.
I'm wondering if my solution is right. My idea is this: At any point of time, the ball may be assumed to be at an incline which is at an angle of θ(kindly see both the pics in the pdf file). The value of θ will continuously change and so will the value of friction.
I'm not able to figure out, why my solution is wrong, if it is wrong .
TL;DR Summary: I came across this question from a Sri Lankan A-level textbook.
Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water.
I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
Does the direction my second finger points in indicate the literal direction of magnetic field at that point in space, or do I need to further use right hand rule or something for a circular path around the finger
Similar threads
- Replies
- 4
- Views
- 408
- Replies
- 22
- Views
- 410
- Replies
- 34
- Views
- 3K
- Replies
- 17
- Views
- 2K
- Replies
- 22
- Views
- 6K
- Replies
- 18
- Views
- 1K
- Replies
- 2
- Views
- 1K
- Replies
- 24
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 2
- Views
- 996
Hot Threads
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
-
How do you calculate the pull of this piston?
- Started by vdance
- Replies: 27
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math