Free-Body Diagrams: Solving for Tension and Weight

  • Thread starter Thread starter unscientific
  • Start date Start date
  • Tags Tags
    Diagram
AI Thread Summary
To draw a free-body diagram accurately, it's essential to represent all forces acting on the object, including weight (W), tension (T), and the normal force (N). The treatment of the object as a particle or one with dimensions affects the diagram's correctness, as two of the three proposed diagrams may be valid based on this consideration. When the object has dimensions, summing torques about a specific point, like the lower right corner of the box, is necessary to ensure stability and rotational equilibrium. Understanding these principles is crucial for correctly analyzing forces in physics problems. Accurate free-body diagrams are fundamental for solving tension and weight issues effectively.
unscientific
Messages
1,728
Reaction score
13
free-body diagram (urgent)

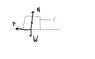
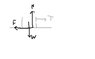
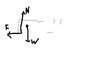
I was wondering how to draw a free body diagram, could u see if this is correct? A body of weight W was pulled along a rough surface, with a string and applied tension T, which one of the following diagrams is correct? N is normal contact force.
 

Attachments

  • option A.jpg
    option A.jpg
    5.7 KB · Views: 366
  • Option B.jpg
    Option B.jpg
    5.2 KB · Views: 386
  • option C.jpg
    option C.jpg
    7.8 KB · Views: 398
Physics news on Phys.org


Sometimes objects are treated as particles, and at other times, objects are considered to have dimensions. So 2 of the three could be correct, depending on whether you consider the object to have dimensions. For the latter case, you'll need to sum torques about the lower right hand corner of the box to check stability and compatability with rotational equilibrium.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Potential Mistake in Free-Body Diagram
Replies
5
Views
2K
Is it friction or tension acting on the person hanging on a rope?
Replies
4
Views
1K
Distributed weight of inclined beam.
Replies
11
Views
3K
Solving Free-Body Diagrams for Moving Nuts on Rods: Tips and Techniques
Replies
9
Views
2K
Tension of string acting on stone moving in horizontal circular motion
Replies
19
Views
3K
Oscillating Spring in a Frictionless pulley system
Replies
23
Views
2K
Free body Diagram of a Plank resting on two Cylinders
Replies
14
Views
3K
Block on top of an inclined plane, with a rough surface, that moves with constant acceleration
Replies
41
Views
4K
Free Body Diagram of Mass-Spring System
Replies
5
Views
1K
Free-body diagram of mechanical system
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top