Gauss' Law confusion

[ZARATHUSTRA]

Ok, so a lot people said that
1. the charge outside of the enclosed surface wouldn't influence the total flux that penetrate the surface
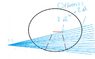
2. q/ε wouldn't change if the charge inside the surface does not change (see my painting, so it can help you understand what i meant)

i was ok with these rules individually at first , but then when i put it together there is a problem, which is when the surface changes, the same electric line would have a different dA⋅E because the angle would be different, so when sum the surface integral, can the value still be the same?(i know i shouldn't question the authority, and i know the answer will be yes, but give me an explanation, and that will be so much helpful to me. Thank you)

 

[DEvens]

The local value can certainly change. So the value of E dot dA at any given location can change. It can change drastically, particularly if a charge is close to the surface.

But you mention total flux. Remember that a flux line starts at a charge and ends at a charge of the opposite sign. (I am being deliberately vague about which sign it starts at and which it ends at because I don't remember.) Or, it runs off to infinity and does not end.

So if you look at your picture with the blue lines you can see what this is about. When a charge is outside a closed surface then a flux line starts outside the surface, enters, moves around a bit, then exits. Each "in" gets exactly one "out." When the charge is inside the closed surface, a flux line starts a the charge and goes out, giving you one net "outs." (Or ends on the charge giving you net "ins" if it is the other sign charge.)

E dot dA will give you the local density of these lines per square cm (or whatever unit of area you are using). This can change drastically, as you can see in your picture with the blue lines being much closer together on one side. The total (gotten through an integral) will count up all the "ins" and all the "outs." And that will be proportional to the total charge inside the surface. The number of flux lines that start (or end) on a charge is proportional to the size of the charge.

 

[rude man]

I think you're implicitly asking for a proof of Gauss' theorem?

 

[ZARATHUSTRA]

I think you're implicitly asking for a proof of Gauss' theorem?

well, kind of, i want to understand a theorem first then apply it, that's how I always do towards math or physics problems

 

[ZARATHUSTRA]

The local value can certainly change. So the value of E dot dA at any given location can change. It can change drastically, particularly if a charge is close to the surface.

But you mention total flux. Remember that a flux line starts at a charge and ends at a charge of the opposite sign. (I am being deliberately vague about which sign it starts at and which it ends at because I don't remember.) Or, it runs off to infinity and does not end.

So if you look at your picture with the blue lines you can see what this is about. When a charge is outside a closed surface then a flux line starts outside the surface, enters, moves around a bit, then exits. Each "in" gets exactly one "out." When the charge is inside the closed surface, a flux line starts a the charge and goes out, giving you one net "outs." (Or ends on the charge giving you net "ins" if it is the other sign charge.)

E dot dA will give you the local density of these lines per square cm (or whatever unit of area you are using). This can change drastically, as you can see in your picture with the blue lines being much closer together on one side. The total (gotten through an integral) will count up all the "ins" and all the "outs." And that will be proportional to the total charge inside the surface. The number of flux lines that start (or end) on a charge is proportional to the size of the charge.

yes, i truly understand that, but my confusion is when the inside surface changed(∑1 changed to ∑2), E⋅dA, especially dA, because the angle between area vector and the local electric field is changed, too. Anyway, thank you very much for your patient explanation, i really appreciate it.

 

[rude man]

well, kind of, i want to understand a theorem first then apply it, that's how I always do towards math or physics problems

Understanding the theorem is not hard. It just states that ∫εE⋅ds integrated over any closed surface (e.g. a balloon ) = q where q is the free charge inside the surface. "Free charge" excludes bound charge as exists in a dielectric. Those are taken care of by ε.
Proof of the theorem is a bigger deal. Essentially it starts with proof of the Divergence Theorem, then invokes either Coulomb's law or one of Maxwell's equations to finally come up with the above. I think, but am not sure, that "Gauss' law" to mathematicians is identically the Divergence theorem, whereas physicists think of "Gauss' law" as the expression above involving free charge.
Anyway, see the attached for a proof (section 5.5).

 

[David Ho]

The local value can certainly change. So the value of E dot dA at any given location can change. It can change drastically, particularly if a charge is close to the surface.

But you mention total flux. Remember that a flux line starts at a charge and ends at a charge of the opposite sign. (I am being deliberately vague about which sign it starts at and which it ends at because I don't remember.) Or, it runs off to infinity and does not end.

So if you look at your picture with the blue lines you can see what this is about. When a charge is outside a closed surface then a flux line starts outside the surface, enters, moves around a bit, then exits. Each "in" gets exactly one "out." When the charge is inside the closed surface, a flux line starts a the charge and goes out, giving you one net "outs." (Or ends on the charge giving you net "ins" if it is the other sign charge.)

E dot dA will give you the local density of these lines per square cm (or whatever unit of area you are using). This can change drastically, as you can see in your picture with the blue lines being much closer together on one side. The total (gotten through an integral) will count up all the "ins" and all the "outs." And that will be proportional to the total charge inside the surface. The number of flux lines that start (or end) on a charge is proportional to the size of the charge.

+ --> -

 

[ZARATHUSTRA]

Understanding the theorem is not hard. It just states that ∫εE⋅ds integrated over any closed surface (e.g. a balloon ) = q where q is the free charge inside the surface. "Free charge" excludes bound charge as exists in a dielectric. Those are taken care of by ε.
Proof of the theorem is a bigger deal. Essentially it starts with proof of the Divergence Theorem, then invokes either Coulomb's law or one of Maxwell's equations to finally come up with the above. I think, but am not sure, that "Gauss' law" to mathematicians is identically the Divergence theorem, whereas physicists think of "Gauss' law" as the expression above involving free charge.
Anyway, see the attached for a proof (section 5.5).[/QUOTE
You are right. Understanding the theorem is not hard, but understanding the proof would take much longer time. Thank you for your help, it's really useful to me.:)