JorgeM
- 30
- 6
- Homework Statement
- Hello everyone.
I need to find out that the gaussian wavepacket is a solution of the Schrödinger equation.
I first tought that It would be so much easier just to calculate the derivatives and to probe that gaussian equation satisfies Schrodinger's equation but it did not result easy at all.
Do you know any book or place where to find this in the simplest way possible (even the demonstration and not just the probe)
I'm relatively new in studying quantum mechanics so many concepts are new to me.
- Relevant Equations
- Schrodinger's equation
The Schrödinger equation I need to prove is this one
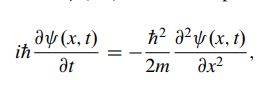
And the Gaussian wavepacket is found here
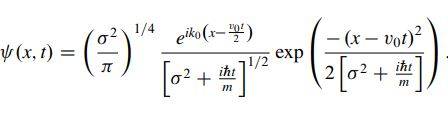
Thanks for your advice.
JorgeM
<Moderator's note: upload images to PhysicsForums. Do not use external image servers.>
And the Gaussian wavepacket is found here
Thanks for your advice.
JorgeM
<Moderator's note: upload images to PhysicsForums. Do not use external image servers.>
Last edited by a moderator: