vcsharp2003
- 913
- 179
- Homework Statement
- Consider the Gaussian surface that surrounds part of charge distribution shown in diagram below.
(a) Which of the charges contribute to the electric field at point P?
(b) Would the value obtained for the flux through the surface, calculated using only the field due to ##q_1## and ##q_2##, be greater than, equal to, or less than that obtained using the total field?
MY PROBLEM IS WITH PART (B)
- Relevant Equations
- ##F = \dfrac {Kq_1q_2} {r^2}##, which is the Coulomb's law
##\phi = \dfrac{\sum {q_i}} {{\epsilon}_0}##, which is Gauss's law
(a) Due to Coulomb's law all charges whether internal or external to Gaussian surface will contribute to the electric field. This is also mentioned as it's correct answer.
(b) The answer is "equal to", which makes no sense to me. It could be greater than, equal to, or less than that obtained using the total field since it will depend on the magnitudes of these individual charges.
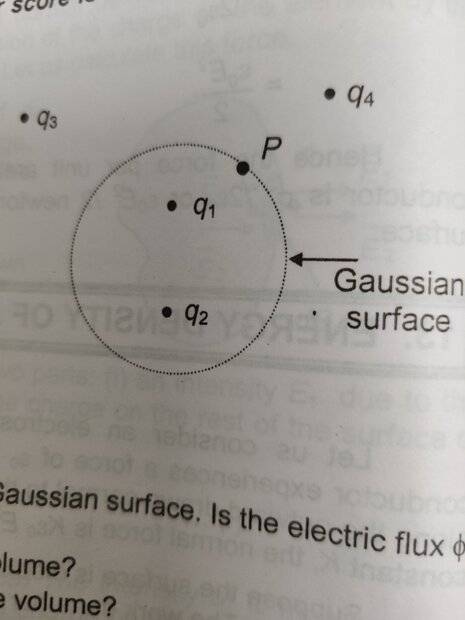
(b) The answer is "equal to", which makes no sense to me. It could be greater than, equal to, or less than that obtained using the total field since it will depend on the magnitudes of these individual charges.