Goodness of fit, Residual STD, chi square

Click For Summary
SUMMARY

The discussion focuses on the use of CasaXPS for modeling synthetic peak models in X-ray photoelectron spectroscopy (XPS) data analysis. The user seeks clarification on how the software calculates the Residual Standard Deviation after each fit iteration, contrasting it with the more commonly used Chi-square and Reduced Chi-square metrics. The user specifically questions the significance of a "Goodness of Fit" value of 286.976 and how to interpret it statistically. The conversation emphasizes the need for a deeper understanding of these statistical measures in the context of CasaXPS.

PREREQUISITES
  • Familiarity with X-ray photoelectron spectroscopy (XPS)
  • Understanding of statistical metrics such as Residual Standard Deviation
  • Knowledge of Chi-square and Reduced Chi-square methods
  • Experience with CasaXPS software for data modeling
NEXT STEPS
  • Research the calculation methods for Residual Standard Deviation in CasaXPS
  • Learn about the interpretation of Chi-square and Reduced Chi-square values
  • Explore statistical significance in the context of goodness-of-fit measures
  • Review CasaXPS manuals for detailed explanations of statistical outputs
USEFUL FOR

Researchers and analysts in the field of X-ray photoelectron spectroscopy, data scientists working with CasaXPS, and anyone interested in understanding statistical metrics for data fitting and analysis.

Dan Zar
Messages
8
Reaction score
0

Homework Statement


Hello,

I am using CasaXPS to model synthetic peak models for X-ray photoelectron spectroscopy data. I am fitting.
The software has a lot of manuals online but they do not explain how they yield a Residual Standard Deviation, after each fit iteration. Most software use Chi-square or Reduced-Chi-squares, which I do not really understand either, but they are more widely used.
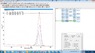
For example,
upload_2016-3-25_3-18-40.png

Whereas most softwares use Reduced Chi squares.
Lastly,Name Block Id Data Set Position FWHM Area St Dev Area %At Conc % St.Dev. Goodness of Fit
sp2 C1s 1-1 12 284.4560 1.1348 135.671 8.38179 54.79 286.976
sp3 C1s 1-1 285.0000 1.2000 89.8416 8.55699 36.28 286.976
sp2-Br C1s 1-1 285.6874 1.2000 14.7421 5.73433 5.95 286.976
C=P C1s 1-1 284.4843 0.9000 7.37342 2.8681 2.98 286.976 I get a report in which the "Goodness of Fit" equals 286.976, how do I transform this number into something statistically significant?
The examples they use on the manuals also happen to have high numbers for "Goodness of Fit"
Thanks a lot.
 

Attachments

  • upload_2016-3-25_3-16-1.png
    upload_2016-3-25_3-16-1.png
    49 KB · Views: 732
Physics news on Phys.org
I think you'll have to check the manual how that property is defined.
 

Similar threads

Graduate The chi square goodness-of-fit test with no degrees of freedom left
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad Small Reduced Chi Squared interpretation
  • · Replies 5 ·
Replies
5
Views
5K
Undergrad About chi-squared and r-squared test for fitting data
  • · Replies 5 ·
Replies
5
Views
9K
Reduced chi square test in physics
  • · Replies 7 ·
Replies
7
Views
7K
High School Chi-squared test stat choosing a critical value
  • · Replies 5 ·
Replies
5
Views
4K
Undergrad Chi-squared and reduced Chi-squared
  • · Replies 1 ·
Replies
1
Views
7K
Graduate What is a Chi-Squared Test Against Weighted Mean?
  • · Replies 2 ·
Replies
2
Views
2K
Graduate Interpreting a very small reduced chi squared value
  • · Replies 6 ·
Replies
6
Views
24K
Calculate the chi-squared probability for the fit
  • · Replies 1 ·
Replies
1
Views
2K
Goodness-of-fit chi-square test on GLM's in R
  • · Replies 9 ·
Replies
9
Views
11K