aim1732
- 428
- 2
How can we graph this inequality - |y|+1/2>=e-|x| ?
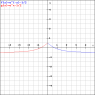
I drew the function(actually a combination of functions) for equality. It would be symmetric in all quadrants and intersect the axes at +ln2 and -ln2(x-axis) and 1/2 and -1/2(y-axis).However since the various graphs are mixed up it is hard pinpoint what region to take.
I have attached one half of the actual graph.
The other half is it's reflection on the x-axis.
I drew the function(actually a combination of functions) for equality. It would be symmetric in all quadrants and intersect the axes at +ln2 and -ln2(x-axis) and 1/2 and -1/2(y-axis).However since the various graphs are mixed up it is hard pinpoint what region to take.
I have attached one half of the actual graph.
The other half is it's reflection on the x-axis.
Attachments
Last edited: