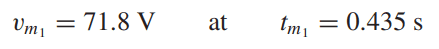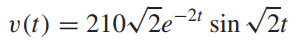paulmdrdo
- 89
- 2
- Homework Statement
- Graph the response v(t)
- Relevant Equations
- SEE THE ATTACHED PHOTO
I'm having difficulty as to how I would produce an approximately graph of the response just by hand. I was able to determine the first maximum by taking the derivative of the response and setting to zero and I'm stuck. How do I know the succeding minimum and maximum of this response? TIA.