Grokking the 1/2 * a * t^2 product

[gibberingmouther]

i am learning physics for fun and also to make taking the actual courses easier. i have a physics textbook because i took physics for my associate's degree but ended up withdrawing because i took too many courses. anyway, i like "connected" knowledge in math though i know it is a bit of a luxury. if i can derive an equation instead of memorizing it all the better!

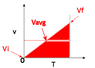
can anyone explain where .5 * a * t^2 comes from? i.e. in x = x0 + v0 * t + 1/2 * a * t^2. i prefer visual/graphical demonstrations, though algebraic is also good. both would be ideal.

edit: sort of related but not as important as my main question, when you have this equation or any other equation that is a function of time giving you your distance in a direction, the graph is a parabola. i think this is correct. so how does a cross section of two cones stacked on top of each other have anything to do with distance? i know it is a weird question but i like this sort of thing.

edit2: okay, i found a derivation on https://mrmackenzie.wikispaces.com/file/view/deriving_equations_of_motion.pdf

still i'll leave this open in case anyone has anything to add or to give input about the second question

 

[Dr.D]

To the best of my knowledge, it is not possible to groke 1/2 a t^2; it just doesn't groke!

 

[gibberingmouther]

as far as the second question, i was in the tub and i realized that the cones touching each other can be made by taking a line in the xy axis and rotating it around a fixed point. so something to do with rotation and lines might be the thing to take away from this.

 

[Vanadium 50]

can anyone explain where .5 * a * t^2 comes from?

at is the velocity at any time. The average velocity if you start from 0 is at/2. Distance is average velocity times time, or at^2/2.

 

[Janus]

Just to add to what Vanadium 50 has already said.
Consider the two graphs below. Both are for velocity over time. The one of the left is for an object at constant velocity and the the one of the right for an object starting at 0 velocity and under a constant acceleration.

In both cases, distance traveled during the interval is the average velocity for the interval multiplied by the time of the interval.
in the constant velocity case, V_i=V_f so the average velocity is equal to both initial and final V. In the accelerating case, V_i=0, so the average velocity for the interval = V_f/2 and since V_f= at, we get at/2 x t = at²/2 for the distance traveled.

You may have also notice that in the left image that the formula V_ft also give you the area under the red velocity line.
If I shade the area under the velocity line for the right image, I get this

Notice that the little red triangle above the V_avg line would fit perfectly into the empty area under the V_avg line, meaning that the shaded area is equal to (V_f/2)t meaning the area under the velocity line also equals the distance traveled in the case when you have acceleration.

 

[Mark44]

To the best of my knowledge, it is not possible to groke 1/2 a t^2; it just doesn't groke!

And to the best of my knowledge, there is no such word as "groke."

The word "grok" was coined by Robert Heinlein in his 1961 SF novel, "Stranger in a Strange Land."

 

[Mark44]

edit: sort of related but not as important as my main question, when you have this equation or any other equation that is a function of time giving you your distance in a direction, the graph is a parabola. i think this is correct. so how does a cross section of two cones stacked on top of each other have anything to do with distance? i know it is a weird question but i like this sort of thing.

I don't understand the reference to "two cones stacked on top of each other."

Here's the standard derivation of the equation $x(t) = x_0 + v_0t + \frac 1 2 at^2$. The derivation uses concepts from calculus, so it might be beyond your current knowledge.

Start from the assumption that an object starts from an initial position at time t = 0 of $x_0$ and an initial velocity of $v_0$, and has a constant acceleration of a (in some appropriate units). Here position x and velocity v are functions of time t; i.e., position = x(t) and velocity = v(t).
Acceleration is defined as the time rate of change of velocity, so $\frac {dv}{dt}$, is equal to a. As an equation, this is $\frac {dv}{dt} = a$
If we integrate both sides, we get $v(t) = at + C_1$
Since $v(0) = v_0$, then $C_1 = v_0$, so we have $v(t) = at + v_0$

Because velocity is the time rate of change of position, we can write the preceding equation as $\frac{dx}{dt} = at + v_0$.
Integrating once again, we get $x(t) = \frac 1 2 at^2 + v_0t + C_2$
Since $x(0) = x_0$, the last equation can be written as $x(t) = \frac 1 2 at^2 + v_0t + x_0$, which is just a rearrangement of your equation in post #1.

College physics courses generally have a prerequisite of calculus...

 

[gibberingmouther]

thanks guys! by "cones touching each other" i was referring to the cones used for getting conic sections - parabolas, hyperbolas, ellipses and circles.

 

[Mark44]

thanks guys! by "cones touching each other" i was referring to the cones used for getting conic sections - parabolas, hyperbolas, ellipses and circles.

OK, gotcha. Technically, though, from the mathematical perspective it's one cone (that has an upper part and a lower part). The curves that are conic sections are defined geometrically by how you slice the cone. If the slice is perpendicular to the cone's axis, and up or down from the vertex, you get a circle. If the slice is parallel to the cone's axis you get the two sheets of a hyperbola, and if the slice is parallel to the sloped sided opposite the slice you get a parabola. If the slice is neither perpendicular to nor parallel to the central axis, and not parallel to the slope opposite from the slice, you get an ellipse.
One of these conic sections shows up in a surprising place: when you sharpen an ordinary pencil in a pencil sharpener, the little curves in the flats of the pencil turn out to be hyperbolic in shape.

 

[phinds]

OK, gotcha. Technically, though, from the mathematical perspective it's one cone (that has an upper part and a lower part). The curves that are conic sections are defined geometrically by how you slice the cone. If the slice is perpendicular to the cone's axis, and up or down from the vertex, you get a circle. If the slice is parallel to the cone's axis you get the two sheets of a hyperbola, and if the slice is parallel to the sloped sided opposite the slice you get a parabola. If the slice is neither perpendicular to nor parallel to the central axis, and not parallel to the slope opposite from the slice, you get an ellipse.
One of these conic sections shows up in a surprising place: when you sharpen an ordinary pencil in a pencil sharpener, the little curves in the flats of the pencil turn out to be hyperbolic in shape.

Just to add to that, the circle is often stated as being the degenerate case of an ellipse, and if you take your slice right through the point where the two parts of the cone touch, you get a point, which is the degenerate case of the circle. If your slice goes up/down and through the vertical axis of the cone, then you get the degenerate case of the hyperbola which is an "X" (two crossed lines).

 

[Dr.D]

And to the best of my knowledge, there is no such word as "groke."

I'm sure you have heard the old saying, "If it ain't groke, don't fix it."

 

[Mark44]

I'm sure you have heard the old saying, "If it ain't groke, don't fix it."

My version of the actual statement is "If we can't fix it, it ain't broke."

 

[phinds]

My version of the actual statement is "If we can't fix it, it ain't broke."

The modern American corporate version seems more to be "it ain't broke, so let's fix it"

 

[rcgldr]

For constant acceleration, calculus is not needed.

Initial and final velocity after time t:
$$v_1 = v_0 + a \ t $$
average velocity
$$av = (v_0 + v_1) / 2 $$
distance versus time:
$$d = av \ t = ((v_0 + v_1)/2) t = (v_0 \ t )/2 +( (v_0 + a \ t) \ t)/2 = v_0 \ t + 1/2 \ a \ t^2 $$