xiphmont
- 1
- 0
"hanging accordian" balanced by opposing moments
This is not a coursework problem, but it looks like one so I'm placing
it here. If this is in error, do correct me. I'm a newbie :-)
Assume an arrangement as below with a fixed surface, five ideal,
weightless beams B_1 through B_5 joined by six axles A_1 through A_6:
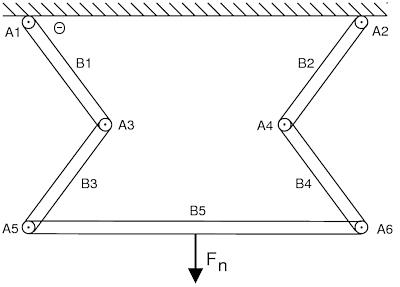
All the vertexes are axles free to rotate in the plane of the diagram
as above. The system is symmetric, so Fn can be split equally between
the ends of B5 and act directly on axles A_5 and A_6. The downward
force results in tension in B3 and B4 and compression in B6:
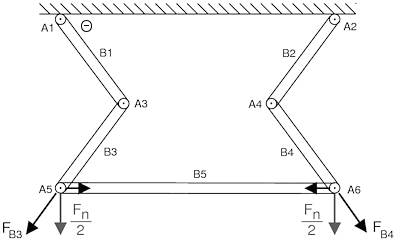
with |F_B4| = |F_B3| = |Fn|*(PI/2-theta) and the compression force in
B6 opposing the x components of the tensions.
The tension in B3 and B4 is transformed into tension forces in B1 and
B2 plus directional forces F_x1 and F_x2:
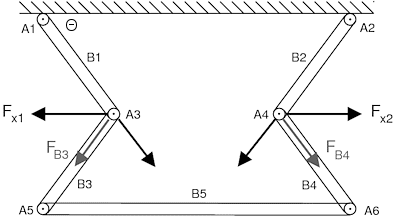
...and F_x1 = 2*Fn*tan(theta), F_x2 = -F_x1. If F_x1 and F_x2 are
opposed the system is static as the tensions are opposed by the fixed
surface at top. I hope this is correct so far.
However, I'm interested in the case where the lower two axles A_5 and
A_6 are pinned (or exactly countersprung, eg, with torsion springs) so
that F_x1 and F_x2 are effectively opposed by moments in B_3 and B_4
about axles A_5 and A_6.
I understand how forces give rise to moments, but my understanding is
quite squishy when it comes to moments giving rise to forces.
Specifically, I know that a moment does not necessarily result in a
force perpendicular to the lever arm, but not really how to wield that
fact.
In any case, my naive solution for t1 is a torque that produces a
force normal to the B_3 lever arm with an x component matching F_x1:
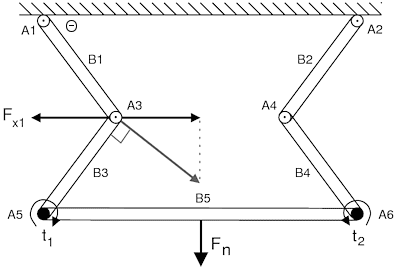
t_1 = -|B_3|*|F_x1|/sin(theta)
with matching symmetric solution for A6.
...this torque is much higher than the torque actually exerted by
F_x1. How is this being balanced? Increased tension in B_1? I don't
know for certain what the actual superimposed direction and magnitude
of the force vector resulting from t_1 is.
I'd appreciate some guidance on the correct solution and even moreso
on the proper way to be approaching it.
This is not a coursework problem, but it looks like one so I'm placing
it here. If this is in error, do correct me. I'm a newbie :-)
Assume an arrangement as below with a fixed surface, five ideal,
weightless beams B_1 through B_5 joined by six axles A_1 through A_6:
All the vertexes are axles free to rotate in the plane of the diagram
as above. The system is symmetric, so Fn can be split equally between
the ends of B5 and act directly on axles A_5 and A_6. The downward
force results in tension in B3 and B4 and compression in B6:
with |F_B4| = |F_B3| = |Fn|*(PI/2-theta) and the compression force in
B6 opposing the x components of the tensions.
The tension in B3 and B4 is transformed into tension forces in B1 and
B2 plus directional forces F_x1 and F_x2:
...and F_x1 = 2*Fn*tan(theta), F_x2 = -F_x1. If F_x1 and F_x2 are
opposed the system is static as the tensions are opposed by the fixed
surface at top. I hope this is correct so far.
However, I'm interested in the case where the lower two axles A_5 and
A_6 are pinned (or exactly countersprung, eg, with torsion springs) so
that F_x1 and F_x2 are effectively opposed by moments in B_3 and B_4
about axles A_5 and A_6.
I understand how forces give rise to moments, but my understanding is
quite squishy when it comes to moments giving rise to forces.
Specifically, I know that a moment does not necessarily result in a
force perpendicular to the lever arm, but not really how to wield that
fact.
In any case, my naive solution for t1 is a torque that produces a
force normal to the B_3 lever arm with an x component matching F_x1:
t_1 = -|B_3|*|F_x1|/sin(theta)
with matching symmetric solution for A6.
...this torque is much higher than the torque actually exerted by
F_x1. How is this being balanced? Increased tension in B_1? I don't
know for certain what the actual superimposed direction and magnitude
of the force vector resulting from t_1 is.
I'd appreciate some guidance on the correct solution and even moreso
on the proper way to be approaching it.