Spoolx
- 38
- 0
Homework Statement
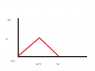
Is the function even, odd, or neither
y(t) = \frac{2At}{w} for 0<t<\frac{w}{2}
y(t) = \frac{-2At}{w}+2A for \frac{w}{2}<t<w
Homework Equations
even function f(-t) = f(t)
off function f(-t) = -f(t)
The Attempt at a Solution
I just don't understand the concept, any help is appreciated.